著者: gpwr
ホドリック・プレスコットフィルターの特長は、遅延がないことです。このフィルターは目的関数を最小化することによって計算されます。
F = Sum((y[i] - x[i])^2,i=0..n-1) + lambda*Sum((y[i+1]+y[i-1]-2*y[i])^2,i=1..n-2)
ここで、x[]は価格、y[]はフィルター値です。以下にフィルターの動作例を示します(HP.mq4ファイル参照)。
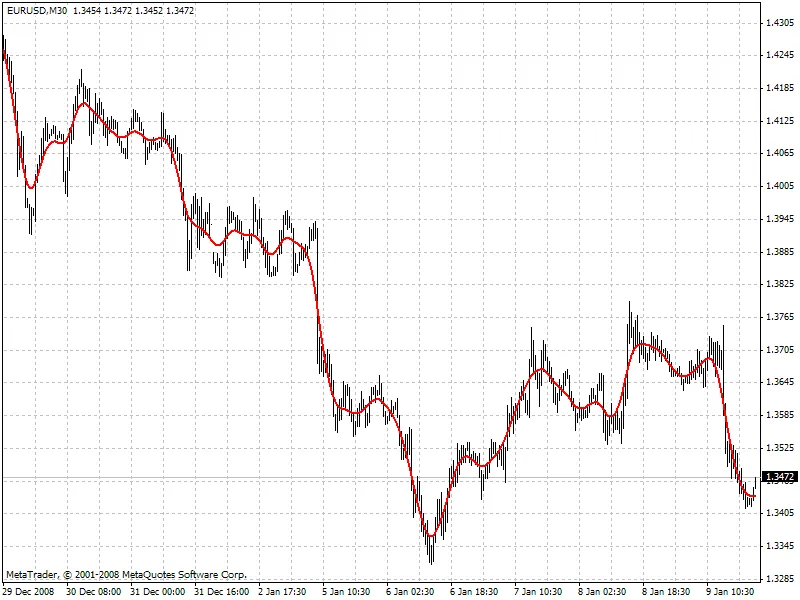
ホドリック・プレスコットフィルターが未来を見る場合、どんな未来の値を示すのでしょうか?この質問に答えるためには、ホドリック・プレスコットフィルターに似た周波数パラメータを持つデジタル低周波フィルターを見つける必要があります。このフィルターは「双子フィルター」の過去の値を使用して直接計算されます。
y[i] = Sum(a[k]*x[i-k],k=0..nx-1) - FIRフィルター
または
y[i] = Sum(a[k]*x[i-k],k=0..nx-1) + Sum(b[k]*y[i-k],k=1..ny) - IIRフィルター
周波数に依存しない遅延Tdel(定常群遅延)を持つ「双子フィルター」を選択する方が良いです。IIRフィルターは不適です。FIRフィルターの場合、周波数に依存しない遅延の条件は以下の通りです:
a[i] = +/-a[nx-1-i], i = 0..nx-1
定常遅延を持つ最も単純なFIRフィルターは単純移動平均(SMA)です:
y[i] = Sum(x[i-k],k=0..nx-1)/nx
nxが奇数の場合、Tdel = (nx-1)/2です。SMAフィルターの値をTdelと等しい数だけ過去にシフトすると、SMAの値はホドリック・プレスコットフィルターの値と一致します。正確な数学的な一致は、2つのフィルターの周波数パラメータの大きな違いにより達成できません(以下のチャート参照):
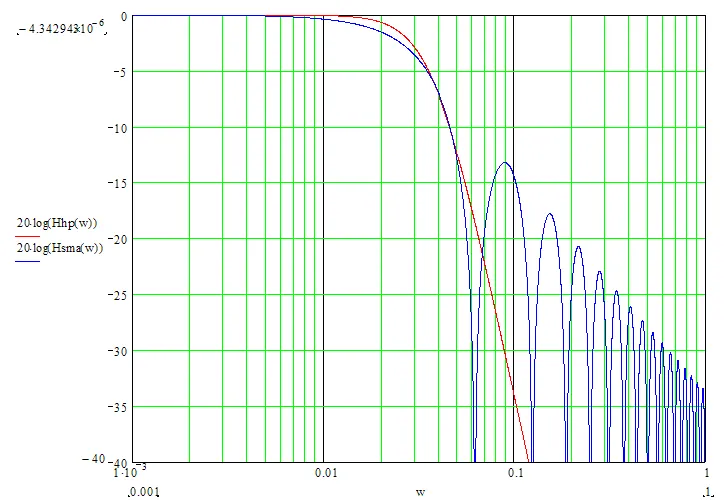
フィルター値の一致を最も近づけるためには、チャネル幅が似ていることをお勧めします(例えば、-6dB)。ホドリック・プレスコットフィルターの-6dBのチャネル幅は以下のように計算されます:
wc = 2*arcsin(0.5/lambda^0.25)。
SMAフィルターの-6dBのチャネル幅は、以下の方程式を用いて数値計算によって計算されます:
|H(w)| = sin(nx*wc/2)/sin(wc/2)/nx = 0.5
以下のチャートは、似たようなチャネル幅を持つ2つのフィルターの値を比較しています:赤 - ホドリック・プレスコットフィルター(FiltPer = 25)、青 - SMA(Period = 15、Shift = -7)。最後の7バーについては、SMAデータがないことに注意してください。なぜなら、未来の価格を知る必要があるからです。一方、ホドリック・プレスコットフィルター(赤)はいくつかの値を示します。シフトされたSMAが未来の価格が現れた後にホドリック・プレスコットフィルターの値を繰り返す場合、これらの値は何になるのでしょうか?
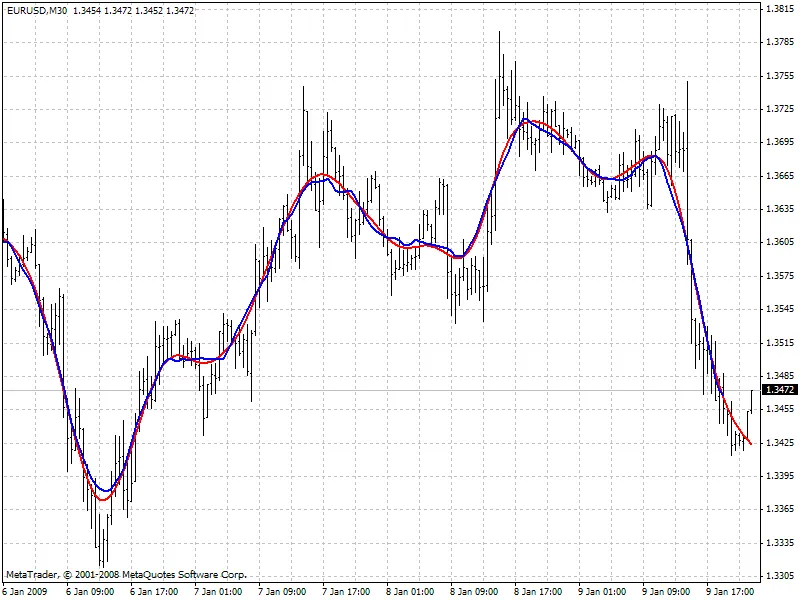
予測アルゴリズム:
このインジケーターには2つの予測方法があります:
方法1:
1. SMAの長さを3に設定し、1バー過去にシフトします。この長さの場合、シフトされたSMAは最後のバー(Bar = 0)に対してのみ存在しません。なぜなら、次の未来価格Close[-1]の値が必要だからです。
2. SMAフィルターのチャネル幅を計算します。ホドリック・プレスコットフィルターと等しくします。lambdaを見つけます。
3. 最後のバーでホドリック・プレスコットフィルターの値HP[0]を計算し、SMA[0]が未知のClose[-1]で同じ値を与えると仮定します。
4. Close[-1] = 3*HP[0] - Close[0] - Close[1]を見つけます。
5. SMAの長さを5に増やします。すべての計算を繰り返し、Close[-2] = 5*HP[0] - Close[-1] - Close[0] - Close[1] - Close[2]を見つけます。指定された数の未来のFutBars価格が計算されるまで続けます。
方法2:
1. SMAの長さを2*FutBars+1に設定し、SMAをFutBarsだけ過去にシフトします。
2. SMAフィルターのチャネル幅を計算します。ホドリック・プレスコットフィルターと等しくします。lambdaを見つけます。
3. 最後のFutBarsでホドリック・プレスコットフィルターの値を計算し、新しい価格が現れるときにSMAが同様に振る舞うと仮定します。
4. Close[-1] = (2*FutBars+1)*HP[FutBars-1] - Sum(Close[i],i=0..2*FutBars-1)、Close[-2] = (2*FutBars+1)*HP[FutBars-2] - Sum(Close[i],i=-1..2*FutBars-2)などを見つけます。
このインジケーターは以下の入力を特徴としています:
- Method - 予測方法
- LastBar - 既存の価格に基づいて予測をチェックする最後のバーの数(LastBar >= 0)
- PastBars - ホドリック・プレスコットフィルターが計算される過去のバーの数(多いほど良い、または少なくともPastBars > 2*FutBars)
- FutBars - 予測される未来の値の数
このインジケーターは予測された値を赤で強調表示します。以下の例では方法1が使用されています:
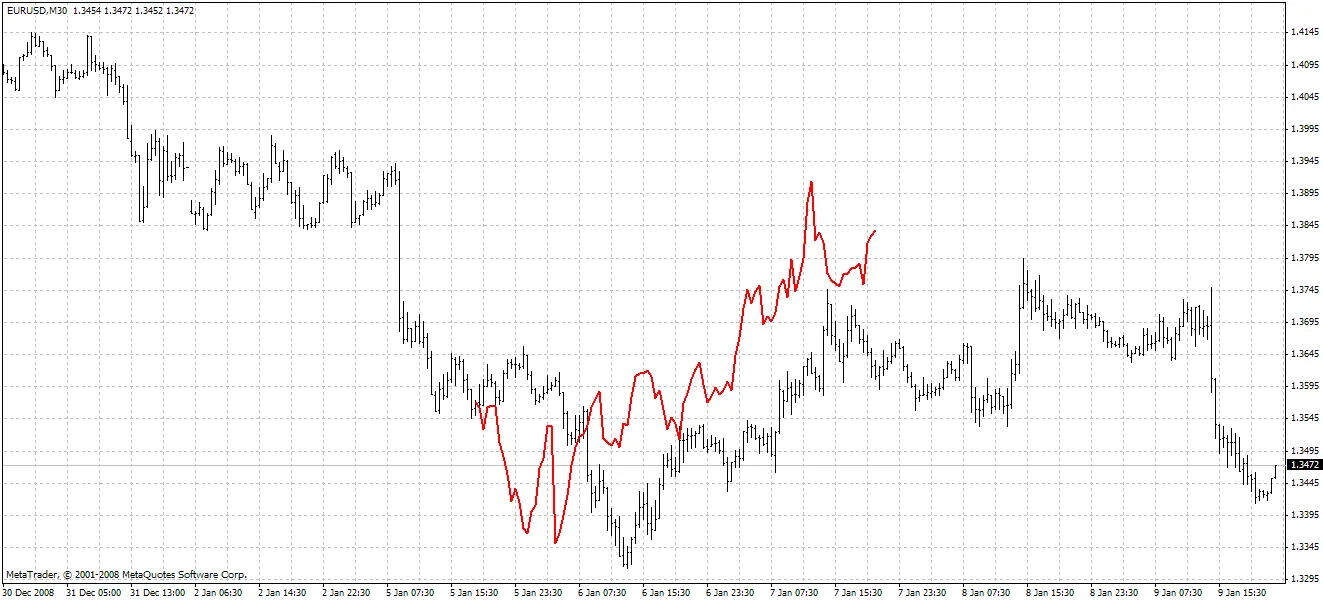
方法2:
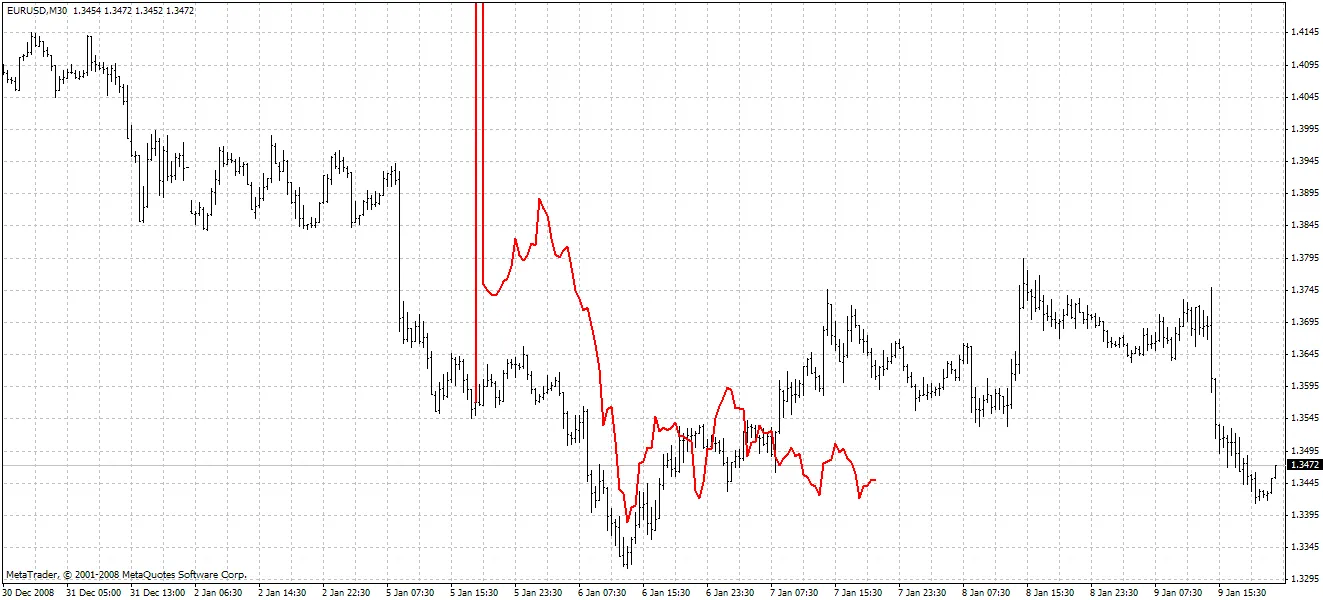
2番目の方法はより正確ですが、最初の予測価格に大きなスパイクが発生することがよくあります。記載された予測方法は、ホドリック・プレスコットフィルターに近い周波数パラメータを持つFIRフィルターを探すことで改善できます。例えば、SMAの代わりにハニング、ブラックマン、カイザーなどの定常遅延を持つフィルターを試してみてください。
著者は、以下のフォーラムセクションに投稿された元のホドリック・プレスコットフィルターのインジケーターに感謝します(ロシア語):
