著者: gpwr
バージョン履歴:
- 2009年6月26日 - 新しいインジケーター「BPNN Predictor with Smoothing.mq4」を追加しました。価格を予測する前にEMAを使ってスムージングを行います。
- 2009年8月20日 - ニューロンの活性化関数の計算コードを修正し、算術例外を防ぎました。BPNN.cppとBPNN.dllを更新。
- 2009年8月21日 - DLLの実行終了時にメモリをクリアする機能を追加しました。BPNN.cppとBPNN.dllを更新。
ニューラルネットワークの簡単な理論:
ニューラルネットワークとは、入力に対する出力の調整可能なモデルです。いくつかの層で構成されています:
- 入力層: 入力データで構成されています。
- 隠れ層: ニューロンと呼ばれる処理ノードで構成されています。
- 出力層: 一つまたは複数のニューロンからなり、ネットワークの出力を生成します。
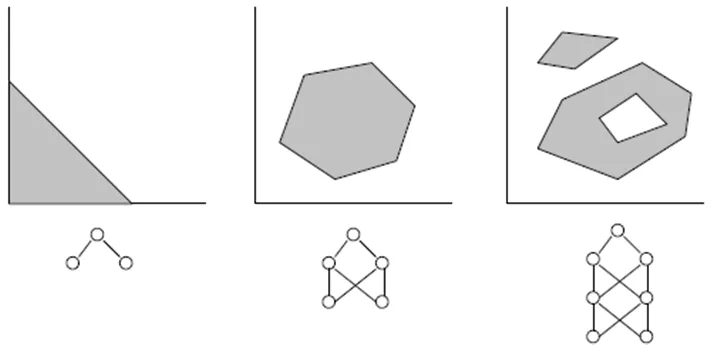
隣接する層のすべてのノードは相互に接続されています。これらの接続はシナプスと呼ばれ、各シナプスにはデータを伝播させるためのスケーリング係数が割り当てられています。これらのスケーリング係数を「重み(w[i][j][k])」と呼びます。フィードフォワードニューラルネットワーク(FFNN)では、データは入力から出力へと伝播します。以下は、1つの入力層、1つの出力層、2つの隠れ層を持つFFNNの例です:
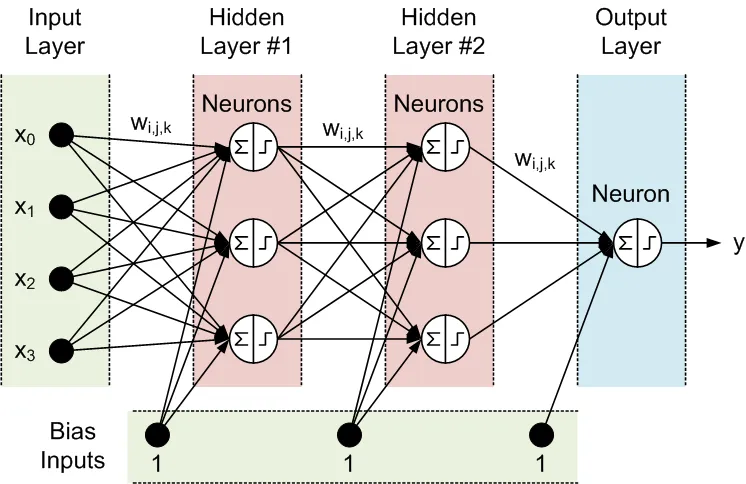
FFNNのトポロジーは、以下のように略記されます: <入力数> - <第一隠れ層のニューロン数> - <第二隠れ層のニューロン数> -...- <出力数>。上記のネットワークは、4-3-3-1ネットワークと呼ばれます。
データはニューロンによって2つのステップで処理されます。円内の合計記号とステップ記号で示されています:
- 全ての入力は関連する重みで掛け合わされ、合計されます。
- 得られた合計はニューロンの活性化関数によって処理され、その出力がニューロンの出力となります。
活性化関数は、ニューラルネットワークモデルに非線形性を与えます。これがなければ、隠れ層を持つ理由がなくなり、ニューラルネットワークは線形自己回帰(AR)モデルになってしまいます。
NN関数のためのライブラリファイルには、以下の3つの活性化関数を選択することができます:
- シグモイド sigm(x)=1/(1+exp(-x)) (#0)
- 双曲線タンジェント tanh(x)=(1-exp(-2x))/(1+exp(-2x)) (#1)
- 有理関数 x/(1+|x|) (#2)
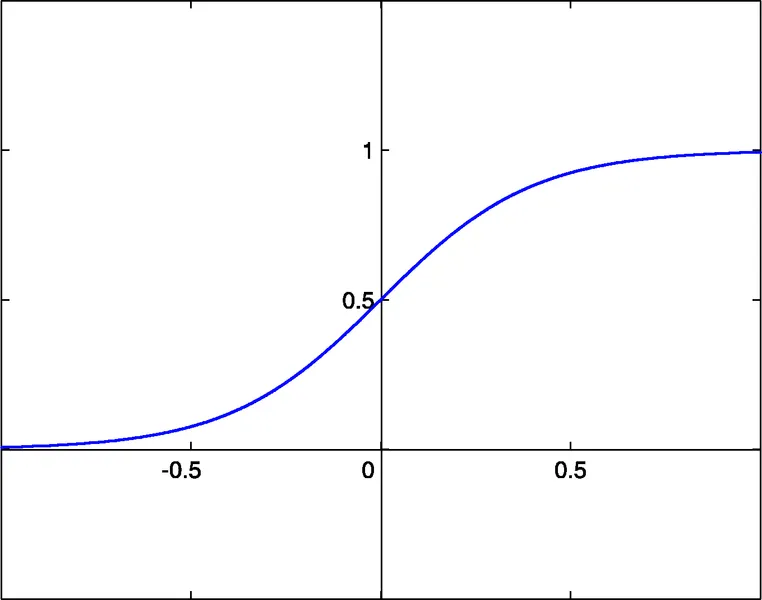
これらの関数の活性化閾値はx=0です。この閾値は、各ニューロンに追加入力されるバイアス入力によってx軸に沿って移動することができます。
入力数、出力数、隠れ層の数、ニューロンの数、シナプスの重みの値は、FFNNを完全に記述します。重みを見つけるためには、ネットワークをトレーニングする必要があります。教師あり学習では、過去の入力データと対応する期待される出力をいくつかのセットとしてネットワークに供給します。重みは、ネットワークの出力と期待される出力の間の誤差を最小限にするように最適化されます。重みの最も単純な最適化手法は、誤差の逆伝播であり、勾配降下法です。このトレーニング関数Train()は、改善された弾性逆伝播法(iRProp+)というこの方法のバリアントを使用します。
http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.17.1332
勾配ベースの最適化手法の主な欠点は、しばしば局所的な最小値を見つけてしまうことです。価格系列のような混沌とした系列では、トレーニング誤差の表面は非常に複雑な形状を持ち、多くの局所的な最小値があります。そのような系列には、遺伝的アルゴリズムが好ましいトレーニング手法です。
同封ファイル:
- BPNN.dll - ライブラリファイル
- BPNN.zip - BPNN.dllをC++でコンパイルするために必要なすべてのファイルのアーカイブ
- BPNN Predictor.mq4 - 将来のオープン価格を予測するインジケーター
- BPNN Predictor with Smoothing.mq4 - スムーズにしたオープン価格を予測するインジケーター
ファイルBPNN.cppにはTrain()とTest()の2つの関数があります。Train()は、供給された過去の入力値と期待される出力に基づいてネットワークをトレーニングするために使用されます。Test()は、Train()で見つけた最適化された重みを使用してネットワークの出力を計算するために使用されます。
Train()の入力(緑)と出力(青)パラメータのリスト:
double inpTrain[] - 入力トレーニングデータ (1D配列、過去のデータが最初)
double outTarget[] - トレーニング用の期待される出力データ (1D配列、過去のデータが最初)
double outTrain[] - トレーニングからのネット出力を保持する1D配列
int ntr - トレーニングセットの数
int UEW - 初期化の際に外部重みを使用するかどうか (1=外部初期重みを使用、0=ランダム使用)
double extInitWt[] - 外部初期重みの3D配列を保持する1D配列
double trainedWt[] - トレーニングされた重みの3D配列を保持する1D配列
int numLayers - 入力、隠れ、出力を含むレイヤーの数
int lSz[] - 各レイヤーのニューロン数。lSz[0]はネット入力の数
int AFT - ニューロンの活性化関数の種類 (0: sigm, 1: tanh, 2: x/(1+x))
int OAF - 出力層の活性化関数を有効にするかどうか (1: 有効、0: 無効)
int nep - 最大トレーニングエポック数
double maxMSE - 最大MSE; maxMSEに達するとトレーニングが停止します。
Test()の入力(緑)と出力(青)パラメータのリスト:
double inpTest[] - 入力テストデータ (1D配列、過去のデータが最初)
double outTest[] - トレーニングからのネット出力を保持する1D配列 (過去のデータが最初)
int ntt - テストセットの数
double extInitWt[] - 外部初期重みの3D配列を保持する1D配列
int numLayers - 入力、隠れ、出力を含むレイヤーの数
int lSz[] - 各レイヤーのニューロン数。lSz[0]はネット入力の数
int AFT - ニューロンの活性化関数の種類 (0: sigm, 1: tanh, 2: x/(1+x))
int OAF - 出力層の活性化関数を有効にするかどうか (1: 有効、0: 無効)
出力層で活性化関数を使用するかどうかは、出力の性質によります。出力がバイナリの場合(分類問題が多い)、出力層で活性化関数を使用すべきです (OAF=1)。活性化関数#0(シグモイド)は0と1の飽和レベルを持ち、活性化関数#1と#2は-1と1のレベルを持ちます。ネットワーク出力が価格予測の場合、出力層での活性化関数は必要ありません (OAF=0)。
NNライブラリの使用例:
BPNN Predictor.mq4 - 将来のオープン価格を予測します。ネットワークの入力は相対価格変化です:
x[i]=Open[test_bar]/Open[test_bar+delay[i]]-1.0
ここで、delay[i]はフィボナッチ数(1,2,3,5,8,13,21..)として計算されます。ネットワークの出力は次の価格の予測相対変化です。出力層での活性化関数はオフ(OAF=0)になっています。
インジケーター入力:
- extern int lastBar - 過去データの最終バー
- extern int futBars - 予測する未来のバーの数
- extern int numLayers - 入力、隠れ、出力を含む層の数 (2..6)
- extern int numInputs - 入力の数
- extern int numNeurons1 - 第一隠れ層または出力層のニューロン数
- extern int numNeurons2 - 第二隠れ層または出力層のニューロン数
- extern int numNeurons3 - 第三隠れ層のニューロン数
- extern int numNeurons4 - 第四隠れ層のニューロン数
- extern int numNeurons5 - 第五隠れ層のニューロン数
- extern int ntr - トレーニングセットの数
- extern int nep - 最大エポック数
- extern int maxMSEpwr - maxMSE=10^maxMSEpwr; トレーニングはmaxMSE未満で停止します
- extern int AFT - 活性化関数のタイプ (0:sigm, 1:tanh, 2:x/(1+x))
インジケーターはチャート上に3つの曲線を描画します:
- 赤色 - 将来の価格の予測
- 黒色 - ネットワークの期待する出力として使用された過去のオープン価格
- 青色 - トレーニング入力に対するネットワークの出力
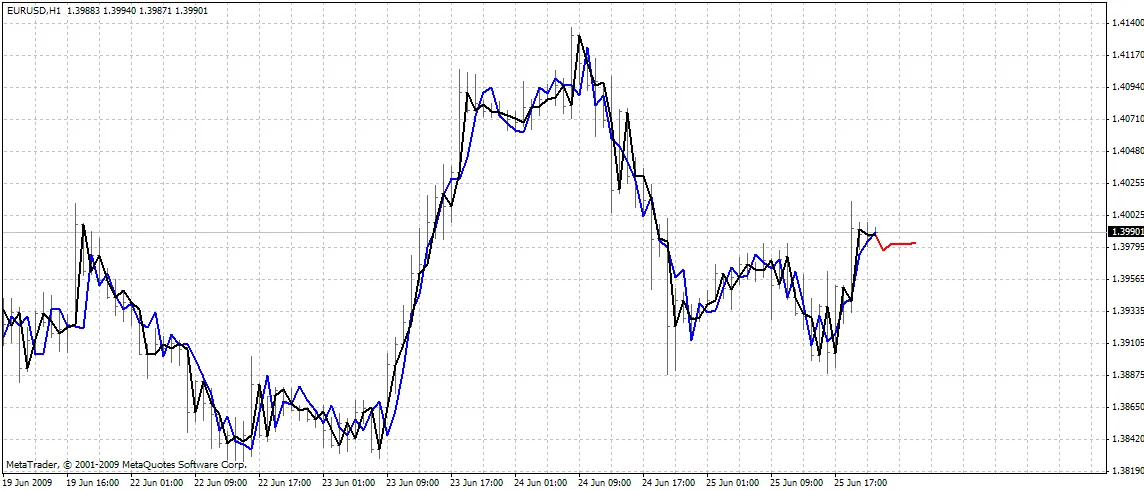
BPNN Predictor.mq4 - 将来のスムーズなオープン価格を予測します。EMAスムージングを使用してsmoothPer期間を取得します。
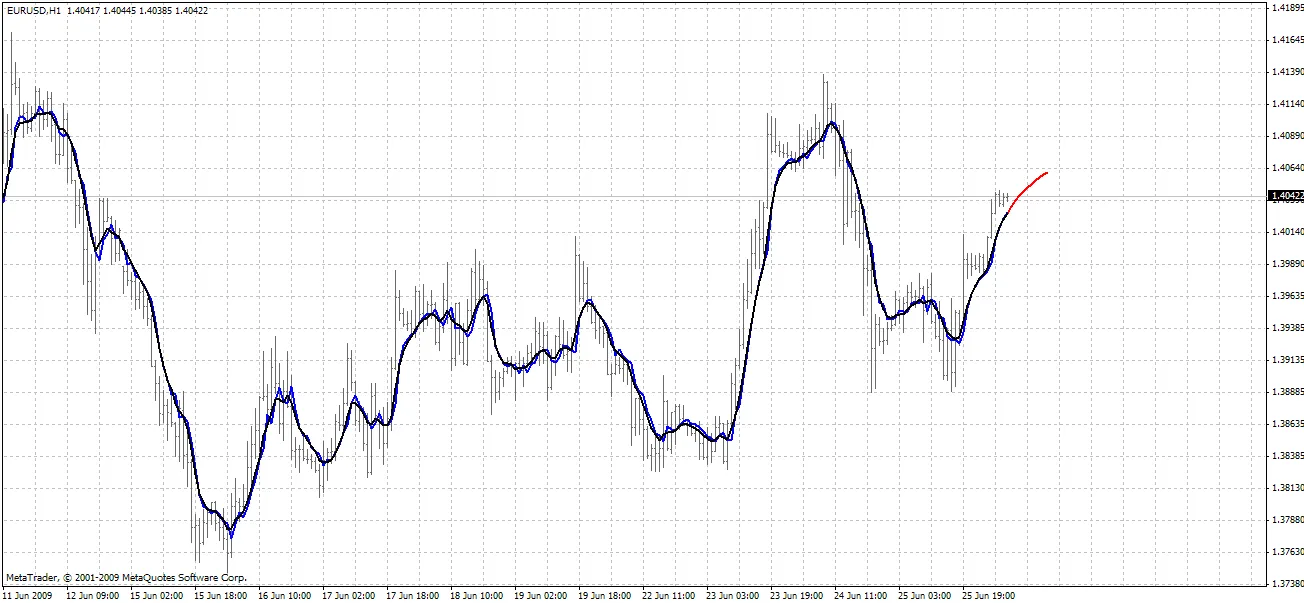
セットアップ手順:
- BPNN.DLLをC:\Program Files\MetaTrader 4\experts\librariesにコピーします。
- MetaTraderで: ツール - オプション - エキスパートアドバイザー - DLLインポートを許可します。
また、BPNN.zip内のソースコードを使用して、自分自身のDLLファイルをコンパイルすることもできます。
推奨事項:
- 層が3つ(numLayers=3: 入力、隠れ、出力)のネットワークで、大多数のケースに対応できます。Cybenko定理(1989)によれば、1つの隠れ層を持つネットワークは、任意の連続した多変量関数を所望の精度で近似することができます。2つの隠れ層を持つネットワークは、任意の不連続な多変量関数を近似することができます。
- 隠れ層の最適なニューロン数は、トライアンドエラーで見つけることができます。文献には次の「経験則」があります: 隠れニューロンの数 = (入力数 + 出力数) / 2、または SQRT(入力数 * 出力数)。トレーニング誤差を追跡し、MetaTraderのエキスパートウィンドウで報告されます。
- 一般化のために、トレーニングセットの数(ntr)は、ネットワークの重みの合計の2-5倍を選択する必要があります。例えば、デフォルトのBPNN Predictor.mq4は12-5-1ネットワークを使用しています。重みの合計は(12+1)*5+6=71です。したがって、トレーニングセットの数(ntr)は少なくとも142であるべきです。一般化と記憶(過学習)の概念は以下のグラフで説明されています。
- ネットワークへの入力データは定常化されるべきです。Forex価格は定常ではありません。また、入力を-1..+1の範囲に正規化することも推奨されます。
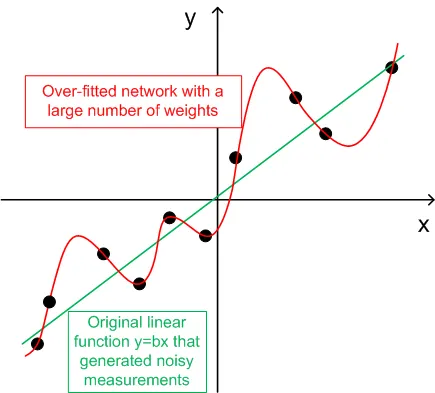
以下のグラフは、ノイズによって歪められた出力を持つ線形関数y=b*x(x-入力、y-出力)を示しています。この追加されたノイズにより、測定された出力(黒い点)は直線から逸脱します。関数y=f(x)はフィードフォワードニューラルネットワークによってモデル化できます。重みが多いネットワークは、測定データにゼロ誤差でフィッティングできます。その挙動は、すべての黒い点を通過する赤い曲線として示されます。しかし、この赤い曲線は元の線形関数y=b*x(緑)とは何の関係もありません。この過学習したネットワークを使用して将来の値を予測すると、追加されたノイズのランダム性のために大きな誤差が発生します。
これらのコードを共有する代わりに、著者は小さなお願いがあります。これらのコードに基づいて利益の出るトレーディングシステムを作成できた場合は、アイデアを私に直接メールで送ってください。vlad1004@yahoo.com
頑張ってください!

コメント 0