今回は、エクストラポレーターというインディケーターについて詳しく解説します。このインディケーターは、選択可能な複数の手法に基づいています。
選べる手法
- メソッド1: フーリエの外挿法 - クイン・フェルナンデスアルゴリズムを用いて周波数を計算
- メソッド2: 自己相関法
- メソッド3: 重み付きバーグ法
- メソッド4: ヘルメ・ニキアス加重関数を用いたバーグ法
- メソッド5: イタクラ-サイト法(幾何学的手法)
- メソッド6: 修正共分散法
メソッド2から6は、線形予測の手法です。線形予測は、過去の値を基に未来の値を線形関数として求めるものです。例えば、価格データx[0]..x[n-1]があるとしましょう。ここで、インデックスが大きいほど最近の価格を示します。未来の価格x[n]は次のように計算されます:
x[n] = -Σ(a[i]*x[n-i], i=1..p)
ここで、a[i=1..p]はモデルの係数、pはモデルの次数です。メソッド2から6は、最後のn-pバーを基に平均二乗誤差を最小化することで係数a[]を求めます。もしもn=2*pのセットの方程式をレヴィンソン・ダービン法で直接解くと、予測誤差をゼロにすることも可能です。この予測法はプラニー法と呼ばれますが、未来の値を予測する際に不安定になるため、今回のインディケーターには含まれていません。
その他の入力パラメータ
- LastBar: 過去データの最後のバーの番号
- PastBars: 未来の値を予測するために使用される過去のバーの数
- LPOrder: 過去のバーの数に対する線形モデルの次数(0..1の範囲)
- FutBars: 予測における未来のバーの数
- HarmNo: メソッド1の最大周波数(0はすべての周波数を意味します)
- FreqTOL: メソッド1の周波数計算の不正確さ(>0.001の場合、収束しません)
- BurgWin: メソッド2の加重関数の数(0=矩形, 1=ハミング, 2=放物線)
このインディケーターは、青いラインでモデルの価格を示し、赤いラインで予測された未来の価格を表示します。
具体例
メソッド1(フーリエ級数の外挿)
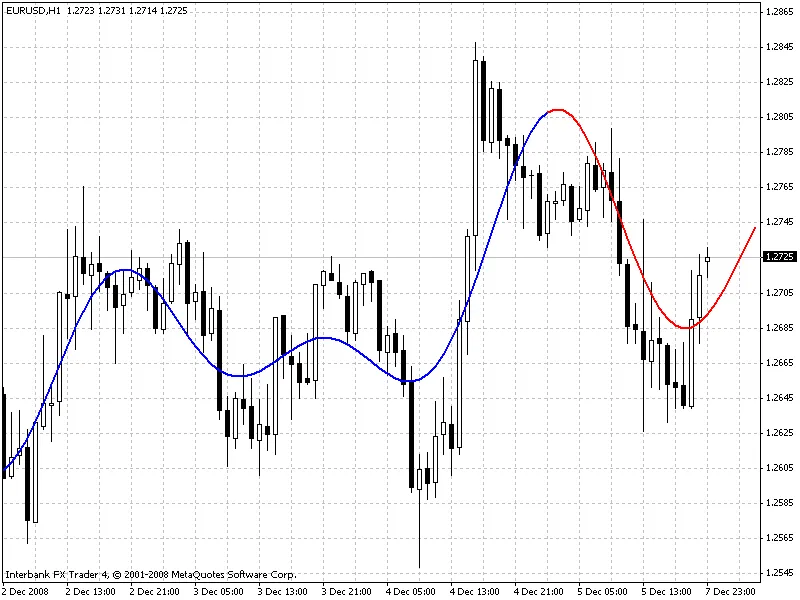
メソッド3(バーグ法)
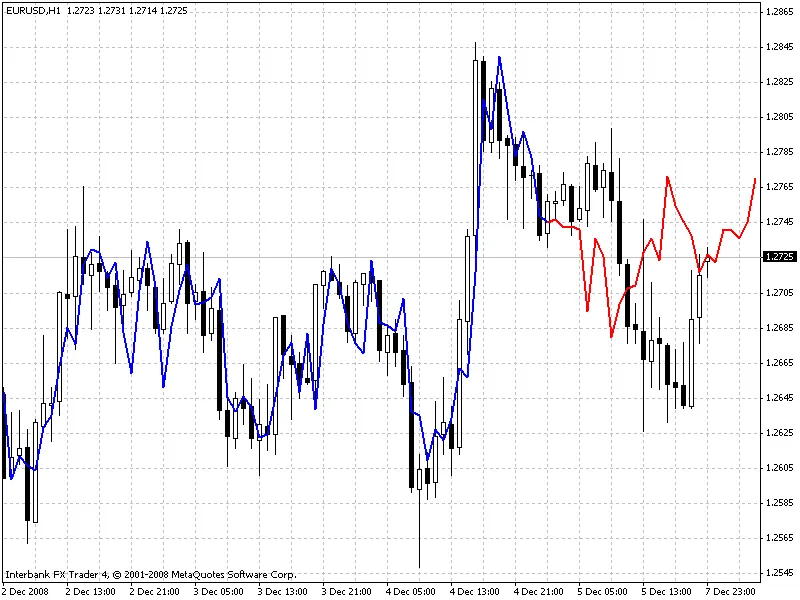
メソッド6(修正共分散法)
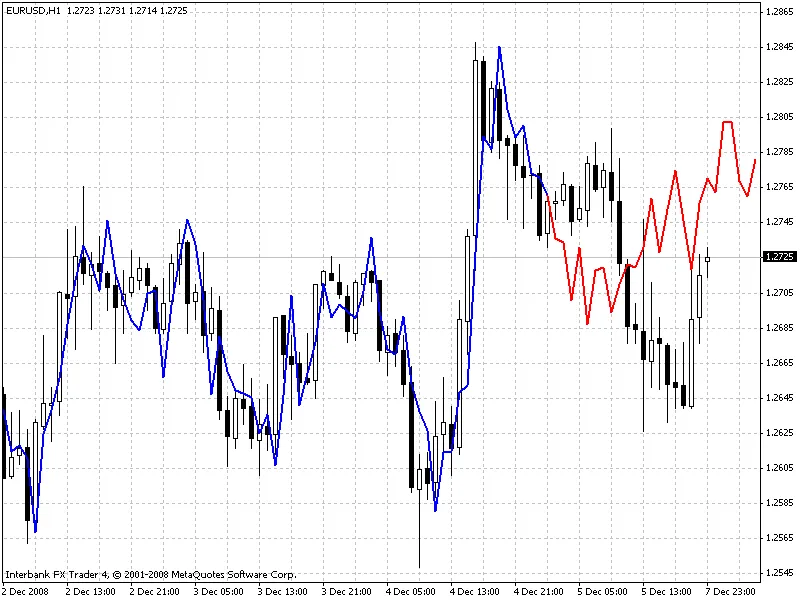
お願い
このインディケーターを使って利益の出るEAを開発した方は、ぜひコード内のメールアドレスまでアイデアを共有していただけると嬉しいです。

コメント 0