Vorhersage von Preisen mit neuronalen Netzwerken: Ein Leitfaden für Trader

Autor: gpwr

Versionshistorie:

26.06.2009 - Neuer Indikator BPNN Predictor mit Glättung.mq4 hinzugefügt, der die Preise vor den Vorhersagen mit EMA glättet.
20.08.2009 - Code zur Berechnung der Neuronenaktivierungsfunktion korrigiert, um arithmetische Ausnahmen zu verhindern; BPNN.cpp und BPNN.dll aktualisiert.
21.08.2009 - Speicherbereinigung am Ende der DLL-Ausführung hinzugefügt; BPNN.cpp und BPNN.dll aktualisiert.

Kurze Theorie der neuronalen Netzwerke:

Ein neuronales Netzwerk ist ein anpassbares Modell von Ausgaben als Funktionen von Eingaben. Es besteht aus mehreren Schichten:

Eingabeschicht, die aus Eingabedaten besteht
Verborgene Schicht, die aus Verarbeitungs-Knoten, auch Neuronen, besteht
Ausgabeschicht, die aus einem oder mehreren Neuronen besteht, deren Ausgaben die Netzwerkausgaben sind.

Alle Knoten benachbarter Schichten sind miteinander verbunden. Diese Verbindungen werden als Synapsen bezeichnet. Jede Synapse hat einen zugewiesenen Skalierungskoeffizienten, mit dem die durch die Synapse propagierten Daten multipliziert werden. Diese Skalierungskoeffizienten werden als Gewichte (w[i][j][k]) bezeichnet. In einem Feed-Forward Neuronalen Netzwerk (FFNN) werden die Daten von den Eingaben zu den Ausgaben propagiert. Hier ist ein Beispiel für ein FFNN mit einer Eingabeschicht, einer Ausgabeschicht und zwei verborgenen Schichten:

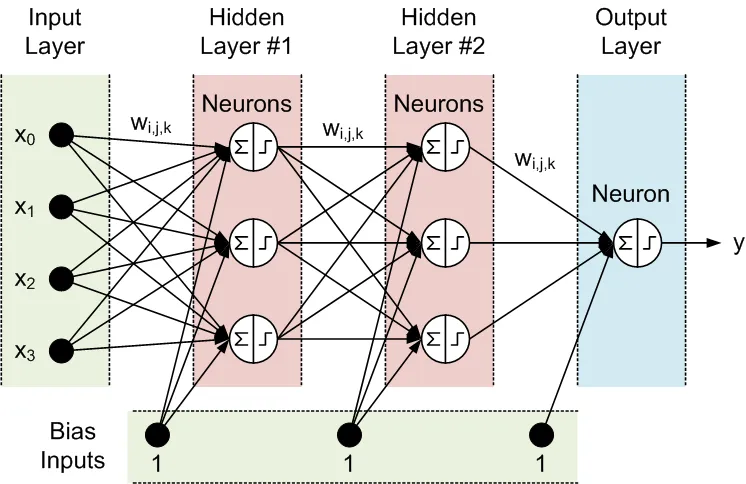
Die Topologie eines FFNN wird häufig folgendermaßen abgekürzt: <# der Eingaben> - <# der Neuronen in der ersten verborgenen Schicht> - <# der Neuronen in der zweiten verborgenen Schicht> -...- <# der Ausgaben>. Das obige Netzwerk kann als 4-3-3-1 Netzwerk bezeichnet werden.

Die Daten werden von den Neuronen in zwei Schritten verarbeitet, die durch ein Summenzeichen und ein Schrittzeichen in dem Kreis dargestellt sind:

Alle Eingaben werden mit den entsprechenden Gewichten multipliziert und summiert.
Die resultierenden Summen werden durch die Aktivierungsfunktion des Neurons verarbeitet, deren Ausgabe die Neuronen-Ausgabe ist.

Es ist die Aktivierungsfunktion des Neurons, die der Struktur des neuronalen Netzwerks Nonlinearität verleiht. Ohne sie wäre es nicht notwendig, verborgene Schichten zu haben, und das neuronale Netzwerk würde zu einem linearen autoregressiven (AR) Modell werden.

Die beigefügten Bibliotheksdateien für NN-Funktionen ermöglichen die Auswahl zwischen drei Aktivierungsfunktionen:

Sigmoid: sigm(x)=1/(1+exp(-x)) (#0)
Hyperbolische Tangens: tanh(x)=(1-exp(-2x))/(1+exp(-2x)) (#1)
Rationale Funktion: x/(1+|x|) (#2)

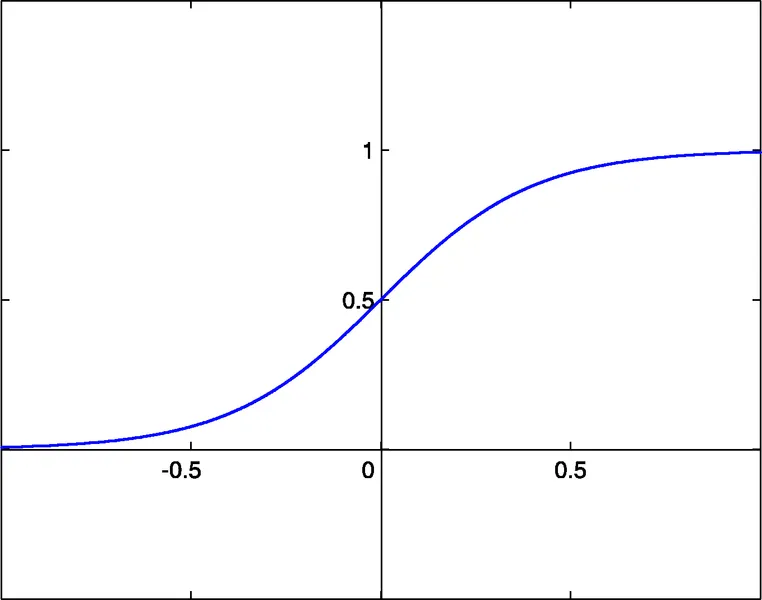
Der Aktivierungsschwellenwert dieser Funktionen ist x=0. Dieser Schwellenwert kann entlang der x-Achse verschoben werden, dank eines zusätzlichen Eingangs jedes Neurons, der als Bias-Eingang bezeichnet wird, dem ebenfalls ein Gewicht zugewiesen ist.

Die Anzahl der Eingaben, Ausgaben, verborgenen Schichten, Neuronen in diesen Schichten und die Werte der Synapsengewichte beschreiben vollständig ein FFNN, d.h. das nichtlineare Modell, das es erstellt. Um die Gewichte zu finden, muss das Netzwerk trainiert werden. Während eines überwachten Trainings werden mehrere Sätze vergangener Eingaben und die entsprechenden erwarteten Ausgaben in das Netzwerk eingespeist. Die Gewichte werden optimiert, um den kleinsten Fehler zwischen den Netzwerkausgaben und den erwarteten Ausgaben zu erreichen. Die einfachste Methode zur Gewichtsoptimierung ist die Backpropagation von Fehlern, die eine Methode des Gradientenabstiegs ist. Die beigefügte Trainingsfunktion Train() verwendet eine Variante dieser Methode, die als Improved Resilient Back-Propagation Plus (iRProp+) bezeichnet wird.

Der Hauptnachteil gradientenbasierter Optimierungsmethoden ist, dass sie oft ein lokales Minimum finden. Für chaotische Serien wie eine Preisserie hat die Trainingsfehleroberfläche eine sehr komplexe Form mit vielen lokalen Minima. Für solche Serien ist ein genetischer Algorithmus eine bevorzugte Trainingsmethode.

Beigefügte Dateien:

BPNN.dll - Bibliotheksdatei
BPNN.zip - Archiv aller Dateien, die zur Kompilierung von BPNN.dll in C++ benötigt werden
BPNN Predictor.mq4 - Indikator zur Vorhersage zukünftiger Eröffnungspreise
BPNN Predictor mit Glättung.mq4 - Indikator zur Vorhersage geglätteter Eröffnungspreise

Datei BPNN.cpp hat zwei Funktionen: Train() und Test().

Train() wird verwendet, um das Netzwerk basierend auf den gelieferten vergangenen Eingaben und erwarteten Ausgaben zu trainieren. Test() wird verwendet, um die Netzwerkausgaben mit den optimierten Gewichten zu berechnen, die von Train() gefunden wurden.

Hier ist die Liste der Eingaben (grün) und Ausgaben (blau) der Train() Funktion:

double inpTrain[] - Eingabetrainingsdaten (1D-Array mit 2D-Daten, die ältesten zuerst)
double outTarget[] - Ausgabedaten für das Training (2D-Daten als 1D-Array, älteste zuerst)
double outTrain[] - Ausgabewerte, um die Netzwerkausgaben aus dem Training zu speichern
int ntr - Anzahl der Trainingssätze
int UEW - Verwendung von externen Gewichten zur Initialisierung (1=verwenden, 0=zufällig)
double extInitWt[] - Eingabewerte zur Speicherung eines 3D-Arrays externer Anfangswerte
double trainedWt[] - Ausgabewerte zur Speicherung eines 3D-Arrays trainierter Gewichte
int numLayers - Anzahl der Schichten einschließlich Eingabe, verborgen und Ausgabe
int lSz[] - Anzahl der Neuronen in den Schichten. lSz[0] ist die Anzahl der Netzwerkeingaben
int AFT - Art der Neuronenaktivierungsfunktion (0:sigm, 1:tanh, 2:x/(1+x))
int OAF - 1 aktiviert die Aktivierungsfunktion für die Ausgabeschicht; 0 deaktiviert sie
int nep - Maximale Anzahl der Trainings-Epochen
double maxMSE - Maximaler MSE; das Training stoppt, sobald maxMSE erreicht wird

Hier ist die Liste der Eingaben (grün) und Ausgaben (blau) der Test() Funktion:

double inpTest[] - Eingabetestdaten (2D-Daten als 1D-Array, älteste zuerst)
double outTest[] - Ausgabewerte, um die Netzwerkausgaben aus dem Training zu speichern (älteste zuerst)
int ntt - Anzahl der Testsätze
double extInitWt[] - Eingabewerte zur Speicherung eines 3D-Arrays externer Anfangswerte
int numLayers - Anzahl der Schichten einschließlich Eingabe, verborgen und Ausgabe
int lSz[] - Anzahl der Neuronen in den Schichten. lSz[0] ist die Anzahl der Netzwerkeingaben
int AFT - Art der Neuronenaktivierungsfunktion (0:sigm, 1:tanh, 2:x/(1+x))
int OAF - 1 aktiviert die Aktivierungsfunktion für die Ausgabeschicht; 0 deaktiviert sie

Ob die Aktivierungsfunktion in der Ausgabeschicht verwendet wird oder nicht, hängt von der Natur der Ausgaben ab. Wenn die Ausgaben binär sind, was oft bei Klassifikationsproblemen der Fall ist, sollte die Aktivierungsfunktion in der Ausgabeschicht verwendet werden (OAF=1). Bitte beachten Sie, dass die Aktivierungsfunktion #0 (sigmoid) 0 und 1 gesättigte Werte hat, während die Aktivierungsfunktionen #1 und #2 Werte von -1 bis 1 haben. Wenn die Netzwerkausgabe eine Preisprognose ist, ist keine Aktivierungsfunktion in der Ausgabeschicht erforderlich (OAF=0).

Beispiele zur Nutzung der NN-Bibliothek:

BPNN Predictor.mq4 - prognostiziert zukünftige Eröffnungspreise. Die Eingaben des Netzwerks sind relative Preisänderungen:

x[i]=Open[test_bar]/Open[test_bar+delay[i]]-1.0

wobei delay[i] als Fibonacci-Zahl berechnet wird (1,2,3,5,8,13,21..). Die Ausgabe des Netzwerks ist die vorhergesagte relative Änderung des nächsten Preises. Die Aktivierungsfunktion ist in der Ausgabeschicht deaktiviert (OAF=0).

Indikatoreingaben:

extern int lastBar - Letzte Kerze in den vergangenen Daten
extern int futBars - Anzahl der zukünftigen Kerzen, die vorhergesagt werden sollen
extern int numLayers - Anzahl der Schichten einschließlich Eingabe, verborgen & Ausgabe (2..6)
extern int numInputs - Anzahl der Eingaben
extern int numNeurons1 - Anzahl der Neuronen in der ersten verborgenen oder Ausgabeschicht
extern int numNeurons2 - Anzahl der Neuronen in der zweiten verborgenen oder Ausgabeschicht
extern int numNeurons3 - Anzahl der Neuronen in der dritten verborgenen oder Ausgabeschicht
extern int numNeurons4 - Anzahl der Neuronen in der vierten verborgenen oder Ausgabeschicht
extern int numNeurons5 - Anzahl der Neuronen in der fünften verborgenen oder Ausgabeschicht
extern int ntr - Anzahl der Trainingssätze
extern int nep - Maximale Anzahl der Epochen
extern int maxMSEpwr - setzt maxMSE=10^maxMSEpwr; Training stoppt < maxMSE
extern int AFT - Art der Aktivierungsfunktion (0:sigm, 1:tanh, 2:x/(1+x))

Der Indikator plottet drei Kurven auf dem Chart:

rote Farbe - Vorhersagen zukünftiger Preise
schwarze Farbe - vergangene Trainingsöffnungspreise, die als erwartete Ausgaben für das Netzwerk verwendet wurden
blaue Farbe - Netzwerkausgaben für die Trainingseingaben

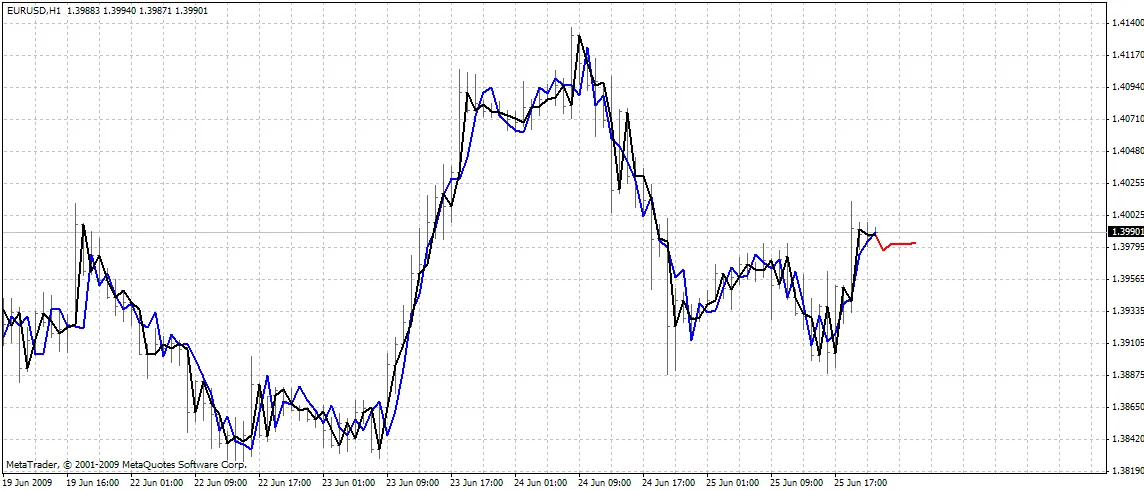
BPNN Predictor mit Glättung.mq4 - prognostiziert zukünftige geglättete Eröffnungspreise. Es verwendet EMA-Glättung mit der Periode smoothPer.

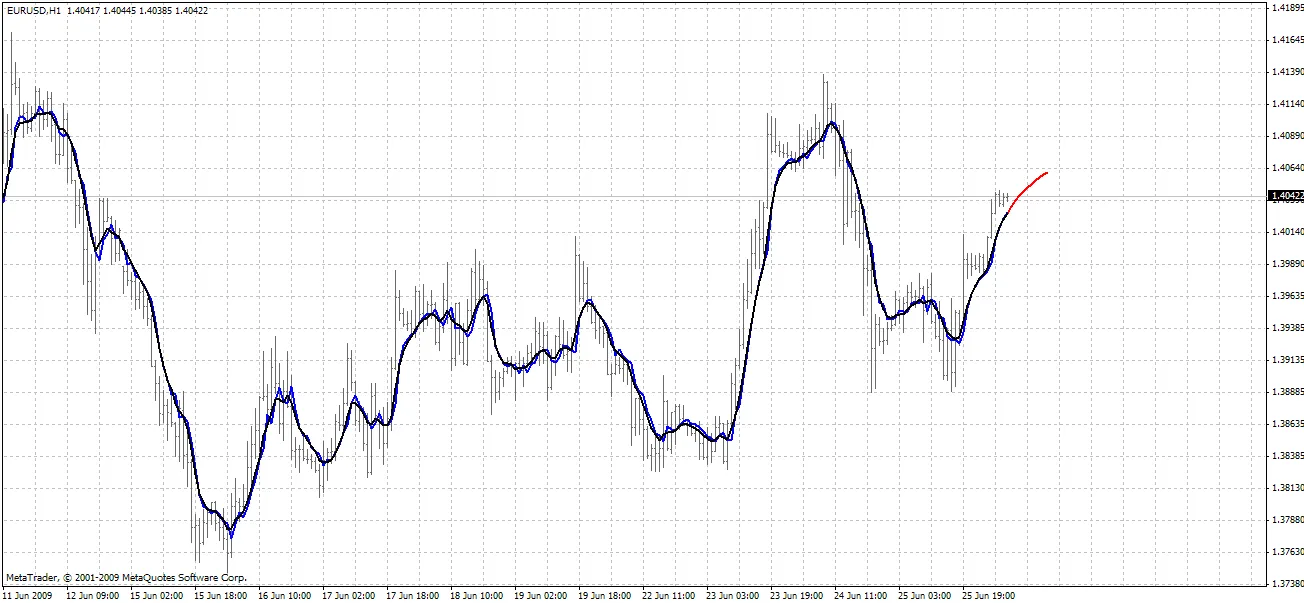
Alles einrichten:

Kopiere die beiliegende BPNN.DLL nach C:\Program Files\MetaTrader 4\experts\libraries
In MetaTrader: Werkzeuge - Optionen - Expert Advisors - DLL-Importe erlauben

Du kannst auch deine eigene DLL-Datei mit den Quellcodes in BPNN.zip kompilieren.

Empfehlungen:

Ein Netzwerk mit drei Schichten (numLayers=3: eine Eingabe-, eine verborgene und eine Ausgabeschicht) reicht für die meisten Fälle aus. Laut dem Cybenko-Theorem (1989) kann ein Netzwerk mit einer verborgenen Schicht jede kontinuierliche, multivariate Funktion auf beliebige Genauigkeit approximieren; ein Netzwerk mit zwei verborgenen Schichten kann jede diskontinuierliche, multivariate Funktion approximieren:
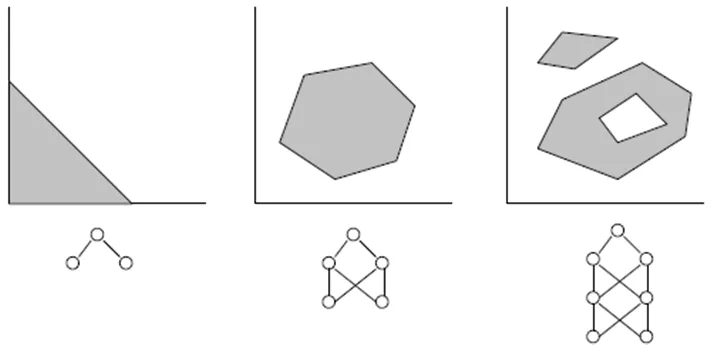
Die optimale Anzahl der Neuronen in der verborgenen Schicht kann durch Ausprobieren gefunden werden. In der Literatur finden sich folgende „Faustregeln“: Anzahl der verborgenen Neuronen = (Anzahl der Eingaben + Anzahl der Ausgaben) / 2 oder SQRT(Anzahl der Eingaben * Anzahl der Ausgaben). Behalte den Training Fehler im Auge, der vom Indikator im Expertenfenster von MetaTrader angezeigt wird.
Zur Generalisierung sollte die Anzahl der Trainingssätze (ntr) 2-5 Mal so hoch sein wie die Gesamtanzahl der Gewichte im Netzwerk. Zum Beispiel verwendet der BPNN Predictor.mq4 standardmäßig ein 12-5-1 Netzwerk. Die Gesamtanzahl der Gewichte beträgt (12+1)*5+6=71. Daher sollte die Anzahl der Trainingssätze (ntr) mindestens 142 betragen. Das Konzept von Generalisierung und Memorisierung (Überanpassung) wird im folgenden Diagramm erklärt.
Die Eingabedaten für das Netzwerk sollten in stationäre Daten umgewandelt werden. Forex-Preise sind nicht stationär. Es wird auch empfohlen, die Eingaben auf den Bereich -1..+1 zu normalisieren.

Das folgende Diagramm zeigt eine lineare Funktion y=b*x (x-Eingabe, y-Ausgabe), deren Ausgaben durch Rauschen gestört sind. Dieses hinzugefügte Rauschen führt dazu, dass die gemessenen Ausgaben (schwarze Punkte) von einer geraden Linie abweichen. Die Funktion y=f(x) kann durch ein Feed-Forward neuronales Netzwerk modelliert werden. Das Netzwerk mit einer großen Anzahl von Gewichten kann an die gemessenen Daten mit null Fehlern angepasst werden. Sein Verhalten wird durch die rote Kurve dargestellt, die durch alle schwarzen Punkte verläuft. Diese rote Kurve hat jedoch nichts mit der ursprünglichen linearen Funktion y=b*x (grün) zu tun. Wenn dieses überangepasste Netzwerk verwendet wird, um zukünftige Werte der Funktion y(x) vorherzusagen, führt dies aufgrund der Zufälligkeit des hinzugefügten Rauschens zu großen Fehlern.

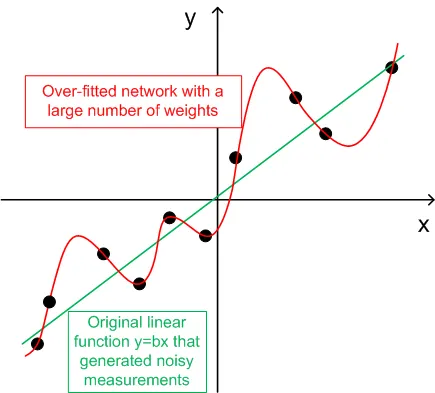
Im Austausch dafür, dass diese Codes geteilt werden, hat der Autor eine kleine Bitte. Wenn du ein profitables Handelssystem auf Basis dieser Codes entwickeln konntest, teile bitte deine Idee direkt mit mir per E-Mail an vlad1004@yahoo.com.

Viel Erfolg!

Vorhersage von Preisen mit neuronalen Netzwerken: Ein Leitfaden für Trader

Beispiele zur Nutzung der NN-Bibliothek:

Verwandte Beiträge