Prédicteur de Prix Futur avec Réseaux de Neurones

Auteur : gpwr

Historique des Versions :

26/06/2009 - ajout d'un nouvel indicateur BPNN Predictor avec Smoothing.mq4, où les prix sont lissés à l'aide de l'EMA avant les prédictions.

20/08/2009 - correction du code calculant la fonction d'activation des neurones pour éviter les exceptions arithmétiques ; mise à jour de BPNN.cpp et BPNN.dll

21/08/2009 - ajout du nettoyage de la mémoire à la fin de l'exécution de la DLL ; mise à jour de BPNN.cpp et BPNN.dll

Brève théorie des Réseaux de Neurones :

Un réseau de neurones est un modèle ajustable des sorties en fonction des entrées. Il se compose de plusieurs couches :

couche d'entrée, qui contient les données d'entrée
couche cachée, composée de nœuds de traitement appelés neurones
couche de sortie, qui se compose d'un ou plusieurs neurones, dont les sorties sont les sorties du réseau.

Tous les nœuds des couches adjacentes sont interconnectés par des connexions appelées synapses. Chaque synapse a un coefficient d'échelle assigné, par lequel les données propagées à travers la synapse sont multipliées. Ces coefficients d'échelle sont appelés poids (w[i][j][k]). Dans un Réseau de Neurones à Propagation Avant (FFNN), les données sont propagées des entrées aux sorties. Voici un exemple de FFNN avec une couche d'entrée, une couche de sortie et deux couches cachées :

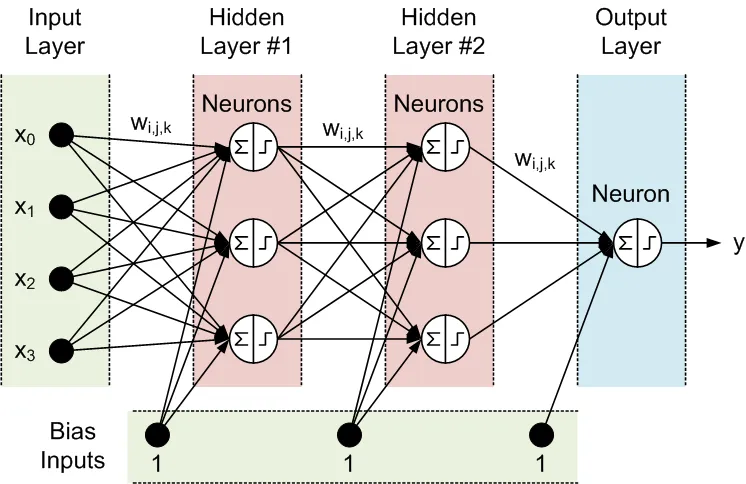
La topologie d'un FFNN est souvent abrégée comme suit : <# d'entrées> - <# de neurones dans la première couche cachée> - <# de neurones dans la deuxième couche cachée> -...- <# de sorties>. Le réseau ci-dessus peut être désigné comme un réseau 4-3-3-1.

Les données sont traitées par les neurones en deux étapes, respectivement représentées dans le cercle par un signe de somme et un signe d'étape :

Tous les entrées sont multipliées par les poids associés et sommées
Les sommes résultantes sont traitées par la fonction d'activation du neurone, dont la sortie est la sortie du neurone.

C'est la fonction d'activation du neurone qui donne une non-linéarité au modèle de réseau de neurones. Sans elle, il n'y a aucune raison d'avoir des couches cachées, et le réseau de neurones devient un modèle autorégressif linéaire (AR).

Les fichiers de bibliothèque joints pour les fonctions NN permettent de sélectionner entre trois fonctions d'activation :

sigmoïde sigm(x)=1/(1+exp(-x)) (#0)
tangente hyperbolique tanh(x)=(1-exp(-2x))/(1+exp(-2x)) (#1)
fonction rationnelle x/(1+|x|) (#2)

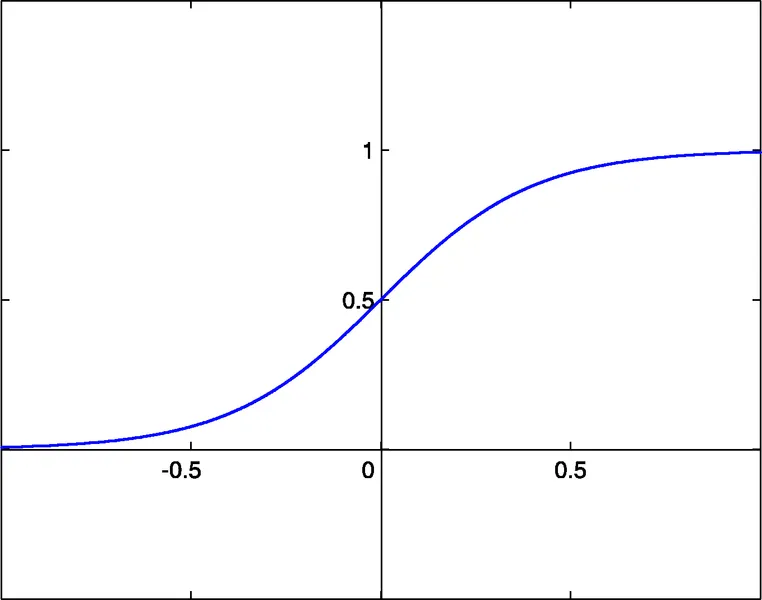
Le seuil d'activation de ces fonctions est x=0. Ce seuil peut être déplacé le long de l'axe x grâce à une entrée supplémentaire de chaque neurone, appelée entrée de biais, qui a également un poids assigné.

Le nombre d'entrées, de sorties, de couches cachées, de neurones dans ces couches, et les valeurs des poids des synapses décrivent complètement un FFNN, c'est-à-dire le modèle non linéaire qu'il crée. Pour trouver les poids, le réseau doit être entraîné. Lors d'un entraînement supervisé, plusieurs ensembles d'entrées passées et les sorties attendues correspondantes sont fournis au réseau. Les poids sont optimisés pour atteindre l'erreur la plus petite entre les sorties du réseau et les sorties attendues. La méthode la plus simple d'optimisation des poids est la rétropropagation des erreurs, qui est une méthode de descente de gradient. La fonction d'entraînement jointe Train() utilise une variante de cette méthode, appelée Rétropropagation Améliorée Plus (iRProp+).

http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.17.1332

Le principal inconvénient des méthodes d'optimisation basées sur le gradient est qu'elles trouvent souvent un minimum local. Pour des séries chaotiques telles qu'une série de prix, la surface d'erreur d'entraînement a une forme très complexe avec de nombreux minima locaux. Pour de telles séries, un algorithme génétique est une méthode d'entraînement préférée.

Fichiers joints :

BPNN.dll - fichier de bibliothèque
BPNN.zip - archive de tous les fichiers nécessaires pour compiler BPNN.dll en C++
BPNN Predictor.mq4 - indicateur prédisant les prix d'ouverture futurs
BPNN Predictor with Smoothing.mq4 - indicateur prédisant les prix d'ouverture lissés

Le fichier BPNN.cpp contient deux fonctions : Train() et Test(). Train() est utilisé pour entraîner le réseau en fonction des valeurs d'entrée passées fournies et des valeurs de sortie attendues. Test() est utilisé pour calculer les sorties du réseau en utilisant les poids optimisés trouvés par Train().

Voici la liste des paramètres d'entrée (vert) et de sortie (bleu) de Train() :

double inpTrain[] - Données d'entraînement d'entrée (tableau 1D contenant des données 2D, les plus anciennes en premier)
double outTarget[] - Données cibles de sortie pour l'entraînement (données 2D sous forme de tableau 1D, les plus anciennes en premier)
double outTrain[] - Tableau 1D de sortie pour contenir les sorties nettes de l'entraînement
int ntr - # d'ensembles d'entraînement
int UEW - Utiliser des poids externes pour l'initialisation (1=utiliser extInitWt, 0=utiliser rnd)
double extInitWt[] - Tableau 1D d'entrée pour contenir un tableau 3D de poids initiaux externes
double trainedWt[] - Tableau 1D de sortie pour contenir un tableau 3D de poids entraînés
int numLayers - # de couches incluant l'entrée, les couches cachées et la sortie
int lSz[] - # de neurones dans les couches. lSz[0] est # des entrées du réseau
int AFT - Type de fonction d'activation des neurones (0:sigm, 1:tanh, 2:x/(1+x))
int OAF - 1 active la fonction d'activation pour la couche de sortie ; 0 désactive
int nep - Max # d'époques d'entraînement
double maxMSE - Max MSE ; l'entraînement s'arrête une fois maxMSE atteint.

Voici la liste des paramètres d'entrée (vert) et de sortie (bleu) de Test() :

double inpTest[] - Données de test d'entrée (données 2D sous forme de tableau 1D, les plus anciennes en premier)
double outTest[] - Tableau 1D de sortie pour contenir les sorties nettes de l'entraînement (les plus anciennes en premier)
int ntt - # d'ensembles de test
double extInitWt[] - Tableau 1D d'entrée pour contenir un tableau 3D de poids initiaux externes
int numLayers - # de couches incluant l'entrée, les couches cachées et la sortie
int lSz[] - # de neurones dans les couches. lSz[0] est # des entrées du réseau
int AFT - Type de fonction d'activation des neurones (0:sigm, 1:tanh, 2:x/(1+x))
int OAF - 1 active la fonction d'activation pour la couche de sortie ; 0 désactive

Que vous utilisiez ou non la fonction d'activation dans la couche de sortie (valeur du paramètre OAF) dépend de la nature des sorties. Si les sorties sont binaires, ce qui est souvent le cas dans les problèmes de classification, alors la fonction d'activation doit être utilisée dans la couche de sortie (OAF=1). Veuillez prêter attention à ce que la fonction d'activation #0 (sigmoïde) a des niveaux saturés de 0 et 1, tandis que les fonctions d'activation #1 et #2 ont des niveaux de -1 et 1. Si la sortie du réseau est une prédiction de prix, alors aucune fonction d'activation n'est nécessaire dans la couche de sortie (OAF=0).

Exemples d'utilisation de la bibliothèque NN :

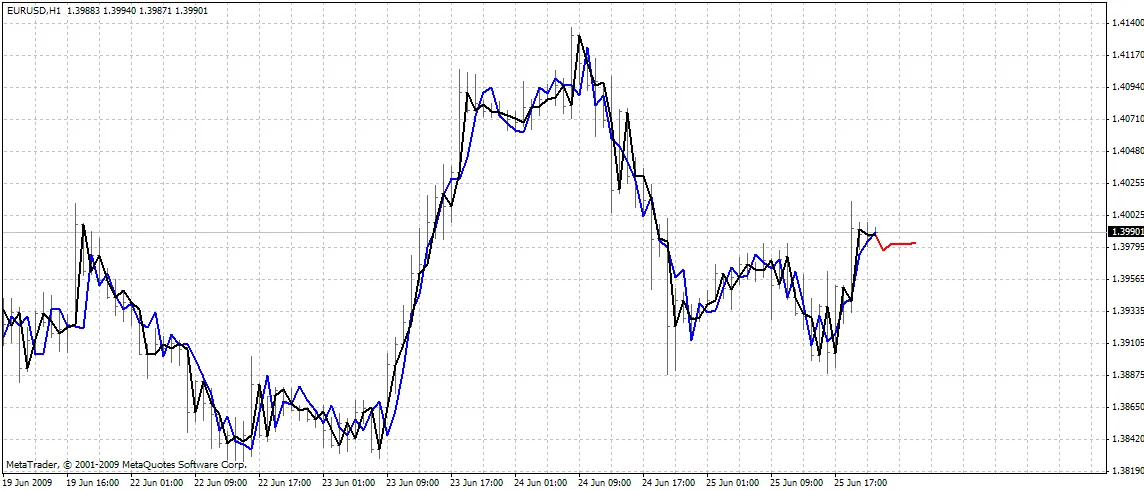
BPNN Predictor.mq4 - prédit les futurs prix d'ouverture. Les entrées du réseau sont les variations de prix relatives :

x[i]=Open[test_bar]/Open[test_bar+delay[i]]-1.0

où delay[i] est calculé comme un nombre de Fibonacci (1,2,3,5,8,13,21..). La sortie du réseau est la variation relative prédite du prochain prix. La fonction d'activation est désactivée dans la couche de sortie (OAF=0).

Paramètres de l'indicateur :

extern int lastBar - Dernière barre dans les données passées
extern int futBars - # de barres futures à prédire
extern int numLayers - # de couches incluant l'entrée, cachées et sortie (2..6)
extern int numInputs - # d'entrées
extern int numNeurons1 - # de neurones dans la première couche cachée ou de sortie
extern int numNeurons2 - # de neurones dans la deuxième couche cachée ou de sortie
extern int numNeurons3 - # de neurones dans la troisième couche cachée ou de sortie
extern int numNeurons4 - # de neurones dans la quatrième couche cachée ou de sortie
extern int numNeurons5 - # de neurones dans la cinquième couche cachée ou de sortie
extern int ntr - # d'ensembles d'entraînement
extern int nep - Max # d'époques
extern int maxMSEpwr - sets maxMSE=10^maxMSEpwr ; l'entraînement s'arrête < maxMSE
extern int AFT - Type de fonction d'activation (0:sigm, 1:tanh, 2:x/(1+x))

L'indicateur trace trois courbes sur le graphique :

couleur rouge - prévisions des prix futurs
couleur noire - prix d'ouverture passés utilisés comme sorties attendues pour le réseau
couleur bleue - sorties du réseau pour les entrées d'entraînement

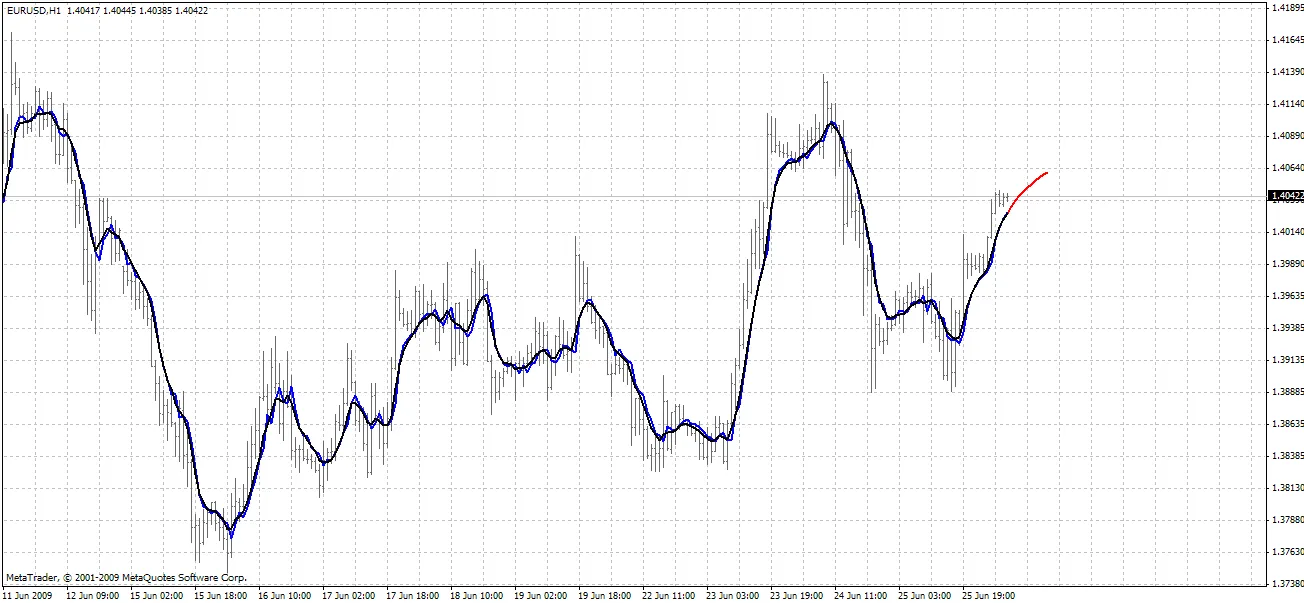
BPNN Predictor.mq4 - prédit les futurs prix d'ouverture lissés. Il utilise un lissage EMA avec une période smoothPer.

Configuration :

Copiez BPNN.DLL dans C:\Program Files\MetaTrader 4\experts\libraries
Dans MetaTrader : Outils - Options - Conseillers Experts - Autoriser les imports DLL

Vous pouvez également compiler votre propre fichier DLL en utilisant les codes sources de BPNN.zip.

Recommandations :

Un réseau avec trois couches (numLayers=3 : une entrée, une cachée et une sortie) est suffisant pour la grande majorité des cas. Selon le Théorème de Cybenko (1989), un réseau avec une couche cachée est capable d'approximer n'importe quelle fonction continue multivariée avec le degré de précision souhaité ; un réseau avec deux couches cachées est capable d'approximer n'importe quelle fonction multivariée discontinue.
Le nombre optimal de neurones dans la couche cachée peut être trouvé par essai et erreur. Les règles empiriques suivantes peuvent être trouvées dans la littérature : # de neurones cachés = (# d'entrées + # de sorties) / 2, ou SQRT(# d'entrées * # de sorties). Gardez une trace de l'erreur d'entraînement, rapportée par l'indicateur dans la fenêtre d'experts de MetaTrader.
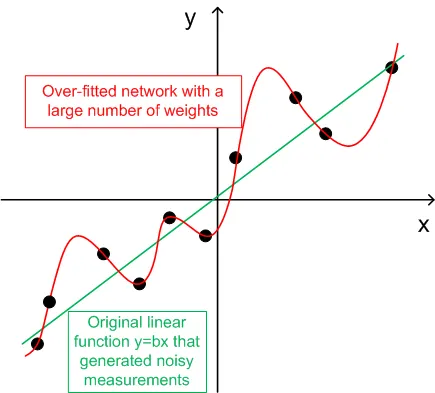
Pour la généralisation, le nombre d'ensembles d'entraînement (ntr) doit être choisi entre 2 et 5 fois le nombre total de poids dans le réseau. Par exemple, par défaut, BPNN Predictor.mq4 utilise un réseau 12-5-1. Le nombre total de poids est (12+1)*5+6=71. Par conséquent, le nombre d'ensembles d'entraînement (ntr) doit être d'au moins 142. Le concept de généralisation et de mémorisation (sur-apprentissage) est expliqué sur le graphique ci-dessous.
Les données d'entrée au réseau doivent être transformées en stationnaires. Les prix Forex ne sont pas stationnaires. Il est également recommandé de normaliser les entrées dans la plage -1..+1.

Le graphique ci-dessous montre une fonction linéaire y=b*x (x-entrée, y-sortie) dont les sorties sont corrompues par du bruit. Ce bruit ajouté fait que les sorties mesurées de la fonction (points noirs) dévient d'une ligne droite. La fonction y=f(x) peut être modélisée par un réseau de neurones à propagation avant. Le réseau avec un grand nombre de poids peut être ajusté aux données mesurées avec une erreur nulle. Son comportement est montré comme la courbe rouge passant par tous les points noirs. Cependant, cette courbe rouge n'a rien à voir avec la fonction linéaire originale y=b*x (verte). Lorsque ce réseau surajusté est utilisé pour prédire de futures valeurs de la fonction y(x), cela entraînera de grandes erreurs en raison de l'aléa du bruit ajouté.

En échange de la diffusion de ces codes, l'auteur a une petite faveur à demander. Si vous avez pu créer un système de trading rentable basé sur ces codes, merci de partager votre idée avec moi en envoyant un email directement à vlad1004@yahoo.com.

Bonne chance !

Prédicteur de Prix Futur avec Réseaux de Neurones

Exemples d'utilisation de la bibliothèque NN :

Articles connexes