Prijsvoorspelling met Neurale Netwerken: Hoe Werkt het?

Auteur: gpwr

Versiegeschiedenis:

26/06/2009 - nieuwe indicator BPNN Predictor met Smoothing.mq4 toegevoegd, waarbij prijzen worden gesmoothed met behulp van EMA voordat voorspellingen worden gedaan.

20/08/2009 - de code voor de neuronactivatiefunctie gecorrigeerd om rekenfouten te voorkomen; BPNN.cpp en BPNN.dll bijgewerkt.

21/08/2009 - geheugen wordt aan het einde van de DLL-uitvoering gewist; BPNN.cpp en BPNN.dll bijgewerkt.

Korte theorie van Neurale Netwerken:

Neuraal netwerk is een aanpasbaar model dat uitgangen als functies van ingangen weergeeft. Het bestaat uit verschillende lagen:

invo laag, bestaande uit invoergegevens
verborgen laag, bestaande uit verwerkingsnodes genaamd neuronen
uitgang laag, bestaande uit een of meerdere neuronen, waarvan de uitgangen de netwerkuitgangen zijn.

Alle knooppunten van aangrenzende lagen zijn met elkaar verbonden. Deze verbindingen worden synapsen genoemd. Elke synaps heeft een toegewezen schalingscoëfficiënt, waarmee de gegevens die door de synaps worden verspreid, worden vermenigvuldigd. Deze schalingscoëfficiënten worden gewichten (w[i][j][k]) genoemd. In een Feed-Forward Neuraal Netwerk (FFNN) worden de gegevens van de ingangen naar de uitgangen verspreid. Hier is een voorbeeld van een FFNN met één invoerlaag, één uitganglaag en twee verborgen lagen:

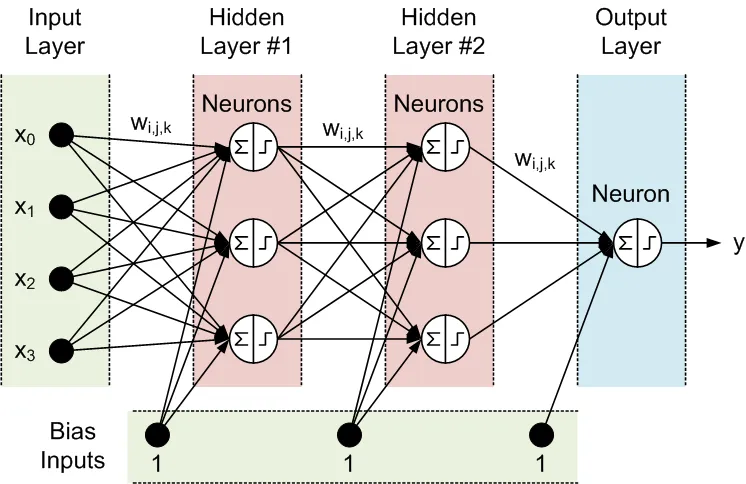
De topologie van een FFNN wordt vaak als volgt afgekort: <aantal ingangen> - <aantal neuronen in de eerste verborgen laag> - <aantal neuronen in de tweede verborgen laag> -...- <aantal uitgangen>. Het bovenstaande netwerk kan worden aangeduid als een 4-3-3-1 netwerk.

De gegevens worden door neuronen in twee stappen verwerkt, zoals weergegeven binnen de cirkel met een somteken en een stapteken:

Alle ingangen worden vermenigvuldigd met de bijbehorende gewichten en opgeteld.
De resulterende sommen worden verwerkt door de activatiefunctie van de neuron, waarvan de uitvoer de uitvoer van de neuron is.

Het is de activatiefunctie van de neuron die de niet-lineariteit aan het neurale netwerkmodel geeft. Zonder deze functie zouden er geen verborgen lagen nodig zijn, en zou het neurale netwerk een lineair autoregressief (AR) model worden.

Bijgevoegde bibliotheekbestanden voor NN-functies maken de selectie mogelijk tussen drie activatiefuncties:

sigmoid sigm(x)=1/(1+exp(-x)) (#0)
hyperbolische tangens tanh(x)=(1-exp(-2x))/(1+exp(-2x)) (#1)
rationele functie x/(1+|x|) (#2)

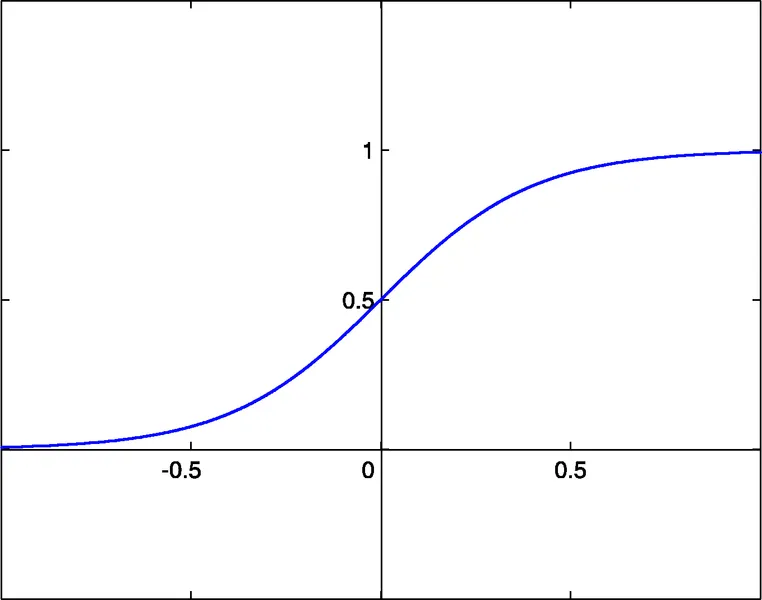
De activatiedrempel van deze functies is x=0. Deze drempel kan langs de x-as worden verplaatst dankzij een extra invoer van elke neuron, genaamd de bias input, die ook een gewicht toegewezen krijgt.

Het aantal ingangen, uitgangen, verborgen lagen, neuronen in deze lagen en de waarden van de synapsgewichten beschrijven volledig een FFNN, dat wil zeggen, het niet-lineaire model dat het creëert. Om gewichten te vinden, moet het netwerk worden getraind. Tijdens supervised training worden verschillende sets van eerdere ingangen en de bijbehorende verwachte uitgangen aan het netwerk gevoed. De gewichten worden geoptimaliseerd om de kleinste fout tussen de netwerkuitgangen en de verwachte uitgangen te bereiken. De eenvoudigste methode voor gewichtsoptimalisatie is de back-propagation van fouten, wat een gradient descent-methode is. De bijgevoegde trainingsfunctie Train() gebruikt een variant van deze methode, genaamd Improved Resilient back-Propagation Plus (iRProp+). Deze methode wordt hier beschreven: http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.17.1332

Het belangrijkste nadeel van gradient-gebaseerde optimalisatiemethoden is dat ze vaak een lokaal minimum vinden. Voor chaotische reeksen zoals een prijsvloer heeft het trainingsfoutoppervlak een zeer complexe vorm met veel lokale minima. Voor dergelijke reeksen is een genetisch algoritme een voorkeurs trainingsmethode.

Bijgevoegde bestanden:

BPNN.dll - bibliotheekbestand
BPNN.zip - archief van alle bestanden die nodig zijn om BPNN.dll in C++ te compileren
BPNN Predictor.mq4 - indicator die toekomstige open prijzen voorspelt
BPNN Predictor met Smoothing.mq4 - indicator die gesmoothde open prijzen voorspelt

Bestand BPNN.cpp heeft twee functies: Train() en Test(). Train() wordt gebruikt om het netwerk te trainen op basis van aangeleverde eerdere input- en verwachte outputwaarden. Test() wordt gebruikt om de netwerkuitgangen te berekenen met behulp van geoptimaliseerde gewichten, gevonden door Train().

Hier is de lijst van invoer (groen) en uitvoer (blauw) parameters van Train():

double inpTrain[] - Input trainingsgegevens (1D-array met 2D-gegevens, oudste eerst)
double outTarget[] - Output doelgegevens voor training (2D-gegevens als 1D-array, oudste eerst)
double outTrain[] - Output 1D-array om netwerkuitgangen van training vast te houden
int ntr - # van trainingssets
int UEW - Gebruik Ext. Gewichten voor initialisatie (1=gebruik extInitWt, 0=gebruik rnd)
double extInitWt[] - Input 1D-array om 3D-array van externe initiële gewichten vast te houden
double trainedWt[] - Output 1D-array om 3D-array van getrainde gewichten vast te houden
int numLayers - # van lagen, inclusief input, verborgen en output
int lSz[] - # van neuronen in lagen. lSz[0] is # van netinvoeren
int AFT - Type van neuronactivatiefunctie (0:sigm, 1:tanh, 2:x/(1+x))
int OAF - 1 schakelt activatiefunctie voor uitganglaag in; 0 schakelt uit
int nep - Max # van trainings-epochs
double maxMSE - Max MSE; training stopt zodra maxMSE is bereikt.

Hier is de lijst van invoer (groen) en uitvoer (blauw) parameters van Test():

double inpTest[] - Input testgegevens (2D-gegevens als 1D-array, oudste eerst)
double outTest[] - Output 1D-array om netwerkuitgangen van training vast te houden (oudste eerst)
int ntt - # van testsets
double extInitWt[] - Input 1D-array om 3D-array van externe initiële gewichten vast te houden
int numLayers - # van lagen, inclusief input, verborgen en output
int lSz[] - # van neuronen in lagen. lSz[0] is # van netinvoeren
int AFT - Type van neuronactivatiefunctie (0:sigm, 1:tanh, 2:x/(1+x))
int OAF - 1 schakelt activatiefunctie voor uitganglaag in; 0 schakelt uit.

Of de activatiefunctie in de uitganglaag al dan niet moet worden gebruikt (waarde van OAF-parameter) hangt af van de aard van de uitgangen. Als de uitgangen binair zijn, wat vaak het geval is bij classificatieproblemen, moet de activatiefunctie in de uitganglaag worden gebruikt (OAF=1). Let op dat activatiefunctie #0 (sigmoid) 0 en 1 verzadigde niveaus heeft, terwijl activatiefunctie #1 en #2 -1 en 1 niveaus hebben. Als de netwerkuitgang een prijsvoorspelling is, is er geen activatiefunctie nodig in de uitganglaag (OAF=0).

Voorbeelden van het gebruik van de NN-bibliotheek:

BPNN Predictor.mq4 - voorspelt toekomstige open prijzen. De ingangen van het netwerk zijn relatieve prijsveranderingen:

x[i]=Open[test_bar]/Open[test_bar+delay[i]]-1.0

waarbij delay[i] wordt berekend als een Fibonacci-getal (1,2,3,5,8,13,21..). De uitvoer van het netwerk is de voorspelde relatieve verandering van de volgende prijs. De activatiefunctie is uitgeschakeld in de uitganglaag (OAF=0).

Indicatorinvoeren:

extern int lastBar - Laatste bar in de historische gegevens
extern int futBars - # van toekomstige bars om te voorspellen
extern int numLayers - # van lagen, inclusief input, verborgen & output (2..6)
extern int numInputs - # van ingangen
extern int numNeurons1 - # van neuronen in de eerste verborgen of uitganglaag
extern int numNeurons2 - # van neuronen in de tweede verborgen of uitganglaag
extern int numNeurons3 - # van neuronen in de derde verborgen of uitganglaag
extern int numNeurons4 - # van neuronen in de vierde verborgen of uitganglaag
extern int numNeurons5 - # van neuronen in de vijfde verborgen of uitganglaag
extern int ntr - # van trainingssets
extern int nep - Max # van epochs
extern int maxMSEpwr - stelt maxMSE=10^maxMSEpwr; training stopt < maxMSE
extern int AFT - Type van activatiefunctie (0:sigm, 1:tanh, 2:x/(1+x))

De indicator plot drie curves op de grafiek:

rode kleur - voorspellingen van toekomstige prijzen
zwarte kleur - eerdere open prijzen, gebruikt als verwachte uitgangen voor het netwerk
blauwe kleur - netwerkuitgangen voor trainingsinvoeren

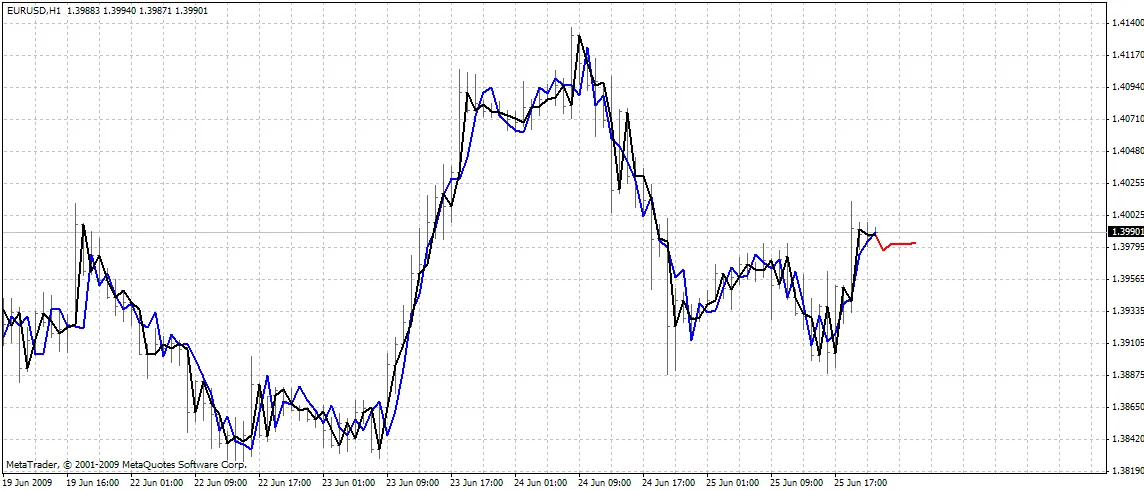
BPNN Predictor.mq4 - voorspelt toekomstige gesmoothde open prijzen. Het gebruikt EMA-smoothing met periode smoothPer.

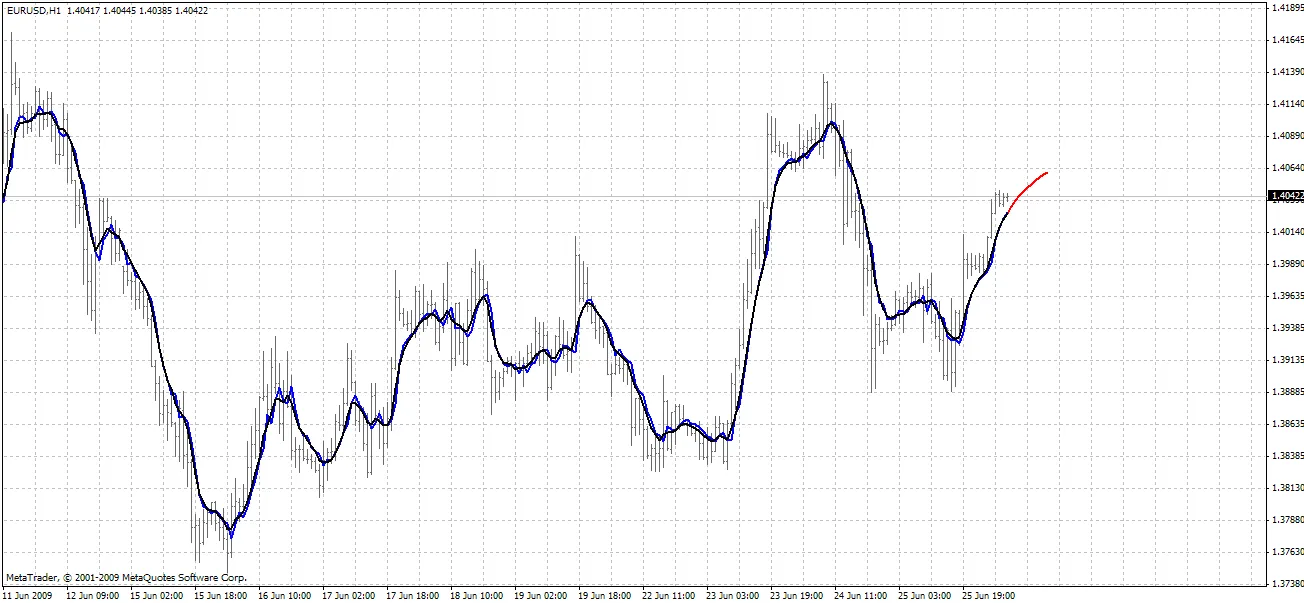
Instellen:

Kopieer de bijgevoegde BPNN.DLL naar C:\Program Files\MetaTrader 4\experts\libraries
In MetaTrader: Hulpmiddelen - Opties - Expert Advisors - Sta DLL-imports toe

Je kunt ook je eigen DLL-bestand compileren met behulp van de bronscodes in BPNN.zip.

Aanbevelingen:

Een netwerk met drie lagen (numLayers=3: één input, één verborgen en één output) is voldoende voor de meeste gevallen. Volgens de Cybenko Theorema (1989) kan een netwerk met één verborgen laag elke continue, multivariate functie tot elke gewenste nauwkeurigheid approximateren; een netwerk met twee verborgen lagen kan elke discontinuïteit, multivariate functie approximateren.
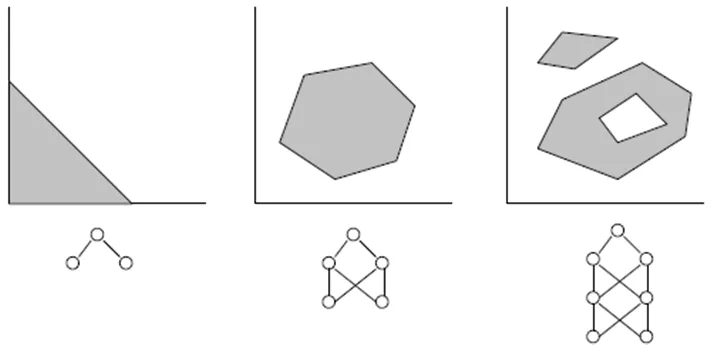
Het optimale aantal neuronen in de verborgen laag kan worden gevonden door middel van trial-and-error. De volgende "regels van duim" kunnen in de literatuur worden gevonden: # van verborgen neuronen = (# van ingangen + # van uitgangen)/2, of SQRT(# van ingangen * # van uitgangen). Houd de trainingsfout bij, die door de indicator in het expertsvenster van MetaTrader wordt gerapporteerd.
Voor generalisatie moet het aantal trainingssets (ntr) 2-5 keer het totale aantal gewichten in het netwerk zijn. Bijvoorbeeld, standaard gebruikt BPNN Predictor.mq4 een 12-5-1 netwerk. Het totale aantal gewichten is (12+1)*5+6=71. Daarom moet het aantal trainingssets (ntr) minstens 142 zijn. Het concept van generalisatie en memorization (over-fitting) wordt hieronder uitgelegd.
De inputgegevens voor het netwerk moeten worden getransformeerd naar stationair. Forex-prijzen zijn niet stationair. Het is ook aan te raden om de ingangen te normaliseren naar een bereik van -1..+1.

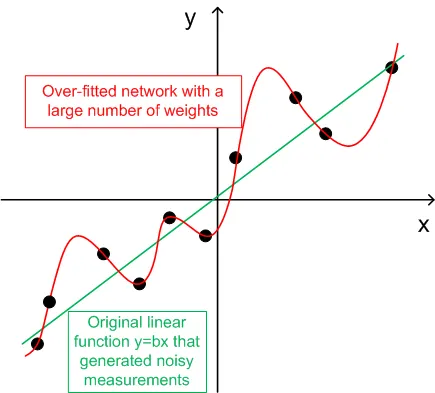
De grafiek hieronder toont een lineaire functie y=b*x (x-input, y-output) waarvan de uitgangen zijn vervormd door ruis. Deze toegevoegde ruis zorgt ervoor dat de gemeten uitgangen (zwarte stippen) van een rechte lijn afwijken. Functie y=f(x) kan worden gemodelleerd door een feedforward-neuraal netwerk. Het netwerk met een groot aantal gewichten kan worden aangepast aan de gemeten gegevens met nul fout. Het gedrag ervan wordt weergegeven als de rode curve die door alle zwarte stippen gaat. Deze rode curve heeft echter niets te maken met de oorspronkelijke lineaire functie y=b*x (groen). Wanneer dit over-gepast netwerk wordt gebruikt om toekomstige waarden van functie y(x) te voorspellen, zal dit leiden tot grote fouten door de willekeurigheid van de toegevoegde ruis.

In ruil voor het delen van deze codes, heeft de auteur een kleine gunst te vragen. Als je een winstgevende handelssysteem hebt kunnen maken op basis van deze codes, deel dan je idee met mij door een e-mail rechtstreeks naar vlad1004@yahoo.com te sturen.

Veel succes!

Prijsvoorspelling met Neurale Netwerken: Hoe Werkt het?

Voorbeelden van het gebruik van de NN-bibliotheek:

Gerelateerde berichten