Previsione dei Prezzi con Reti Neurali: Un Guida per Trader

Autore:

gpwr

Storia delle Versioni:

26/06/2009 - Aggiunto un nuovo indicatore BPNN Predictor con Smoothing.mq4, in cui i prezzi vengono smussati utilizzando l'EMA prima delle previsioni.

20/08/2009 - Corretto il codice che calcolava la funzione di attivazione dei neuroni per prevenire eccezioni aritmetiche; aggiornati BPNN.cpp e BPNN.dll

21/08/2009 - Aggiunta la pulizia della memoria al termine dell'esecuzione della DLL; aggiornati BPNN.cpp e BPNN.dll

Breve Teoria delle Reti Neurali:

La rete neurale è un modello adattabile degli output in funzione degli input. È composta da diversi strati:

strato di input, che consiste nei dati di input
strato nascosto, composto da nodi di elaborazione chiamati neuroni
strato di output, che consiste in uno o più neuroni, i cui output sono i risultati della rete.

Tutti i nodi degli strati adiacenti sono interconnessi. Queste connessioni sono chiamate sinapsi. Ogni sinapsi ha un coefficiente di scaling assegnato, con cui i dati propagati attraverso la sinapsi vengono moltiplicati. Questi coefficienti di scaling sono chiamati pesi (w[i][j][k]). In una Rete Neurale Feed-Forward (FFNN), i dati vengono propagati dagli input agli output. Ecco un esempio di FFNN con uno strato di input, uno di output e due strati nascosti:

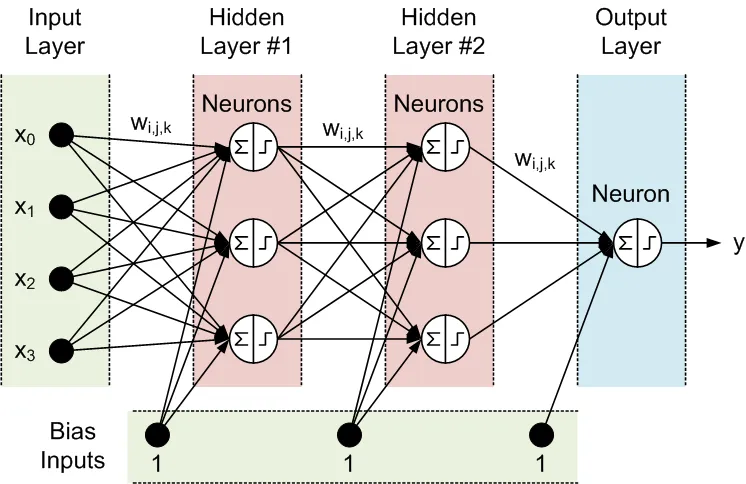
La topologia di una FFNN è spesso abbreviata come segue: <# di input> - <# di neuroni nel primo strato nascosto> - <# di neuroni nel secondo strato nascosto> -...- <# di output>. La rete sopra può essere chiamata una rete 4-3-3-1.

I dati vengono elaborati dai neuroni in due fasi, illustrate nel cerchio da un segno di somma e un segno di passo:

Tutti gli input vengono moltiplicati per i pesi associati e sommati.
Le somme risultanti vengono elaborate dalla funzione di attivazione del neurone, il cui output è l'output del neurone.

È la funzione di attivazione del neurone a conferire non linearità al modello di rete neurale. Senza di essa, non ci sarebbe motivo di avere strati nascosti, e la rete neurale diventerebbe un modello autoregressivo lineare (AR).

I file di libreria inclusi per le funzioni NN consentono la selezione tra tre funzioni di attivazione:

sigmoide sigm(x)=1/(1+exp(-x)) (#0)
tangente iperbolica tanh(x)=(1-exp(-2x))/(1+exp(-2x)) (#1)
funzione razionale x/(1+|x|) (#2)

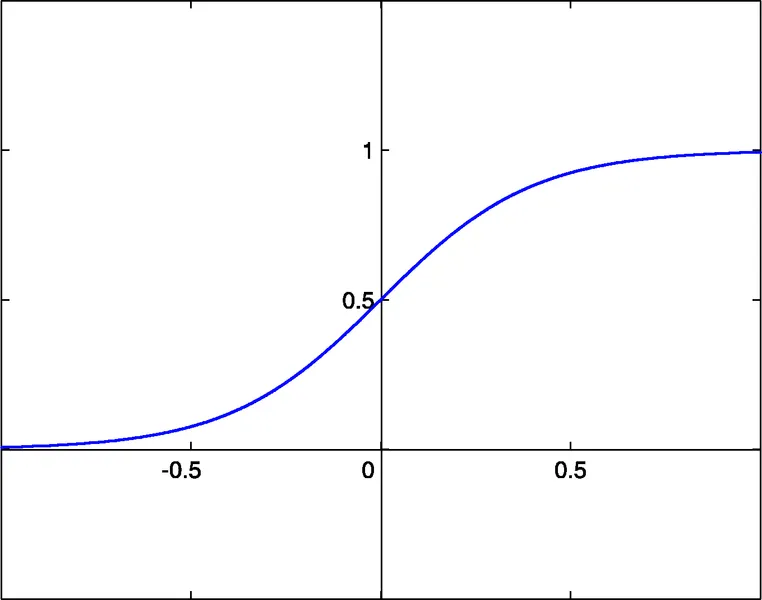
La soglia di attivazione di queste funzioni è x=0. Questa soglia può essere spostata lungo l'asse x grazie a un ulteriore input di ciascun neurone, chiamato input di bias, che ha anche un peso assegnato.

Il numero di input, output, strati nascosti, neuroni in questi strati e i valori dei pesi delle sinapsi descrivono completamente una FFNN, ovvero il modello non lineare che essa crea. Per trovare i pesi, la rete deve essere addestrata. Durante un addestramento supervisionato, diversi set di input passati e i corrispondenti output attesi vengono forniti alla rete. I pesi vengono ottimizzati per ridurre al minimo l'errore tra gli output della rete e gli output attesi. Il metodo più semplice di ottimizzazione dei pesi è il back-propagation degli errori, che è un metodo di discesa del gradiente. La funzione di addestramento inclusa Train() utilizza una variante di questo metodo, chiamata Improved Resilient back-Propagation Plus (iRProp+).

Il principale svantaggio dei metodi di ottimizzazione basati sul gradiente è che spesso trovano un minimo locale. Per serie caotiche come una serie di prezzi, la superficie dell'errore di addestramento ha una forma molto complessa con molti minimi locali. Per tali serie, un algoritmo genetico è un metodo di addestramento preferito.

File inclusi:

BPNN.dll - file di libreria
BPNN.zip - archivio di tutti i file necessari per compilare BPNN.dll in C++
BPNN Predictor.mq4 - indicatore che predice i futuri prezzi di apertura
BPNN Predictor con Smoothing.mq4 - indicatore che predice i prezzi di apertura smussati

Il file BPNN.cpp ha due funzioni: Train() e Test().
Train() viene utilizzata per addestrare la rete in base ai valori di input e output attesi forniti. Test() viene utilizzata per calcolare gli output della rete utilizzando i pesi ottimizzati trovati da Train().

Ecco l'elenco dei parametri di input (in verde) e output (in blu) di Train():

double inpTrain[] - Dati di input per l'addestramento (array 1D che contiene dati 2D, i più vecchi per primi)
double outTarget[] - Dati target di output per l'addestramento (dati 2D come array 1D, i più vecchi per primi)
double outTrain[] - Array 1D di output per contenere gli output netti dall'addestramento
int ntr - # di set di addestramento
int UEW - Usa pesi esterni per l'inizializzazione (1=usa extInitWt, 0=usa rnd)
double extInitWt[] - Array 1D per contenere un array 3D di pesi iniziali esterni
double trainedWt[] - Array 1D di output per contenere un array 3D di pesi addestrati
int numLayers - # di strati inclusi input, nascosti e output
int lSz[] - # di neuroni negli strati. lSz[0] è # di input netti
int AFT - Tipo di funzione di attivazione dei neuroni (0:sigm, 1:tanh, 2:x/(1+x))
int OAF - 1 abilita la funzione di attivazione per lo strato di output; 0 disabilita
int nep - Max # di epoche di addestramento
double maxMSE - Max MSE; l'addestramento si interrompe una volta raggiunta maxMSE.

Ecco l'elenco dei parametri di input (in verde) e output (in blu) di Test():

double inpTest[] - Dati di input per il test (dati 2D come array 1D, i più vecchi per primi)
double outTest[] - Array 1D di output per contenere gli output netti dall'addestramento (i più vecchi per primi)
int ntt - # di set di test
double extInitWt[] - Array 1D per contenere un array 3D di pesi iniziali esterni
int numLayers - # di strati inclusi input, nascosti e output
int lSz[] - # di neuroni negli strati. lSz[0] è # di input netti
int AFT - Tipo di funzione di attivazione dei neuroni (0:sigm, 1:tanh, 2:x/(1+x))
int OAF - - 1 abilita la funzione di attivazione per lo strato di output; 0 disabilita

Se utilizzare o meno la funzione di attivazione nello strato di output (valore del parametro OAF) dipende dalla natura degli output. Se gli output sono binari, come spesso accade nei problemi di classificazione, allora la funzione di attivazione dovrebbe essere utilizzata nello strato di output (OAF=1). Si prega di notare che la funzione di attivazione #0 (sigmoide) ha livelli saturi 0 e 1, mentre le funzioni di attivazione #1 e #2 hanno livelli -1 e 1. Se l'output della rete è una previsione di prezzo, allora non è necessaria alcuna funzione di attivazione nello strato di output (OAF=0).

Esempi di utilizzo della libreria NN:

BPNN Predictor.mq4 - prevede i futuri prezzi di apertura. Gli input della rete sono i cambiamenti relativi dei prezzi:

x[i]=Open[test_bar]/Open[test_bar+delay[i]]-1.0

dove delay[i] viene calcolato come un numero di Fibonacci (1,2,3,5,8,13,21..). L'output della rete è il cambiamento relativo previsto del prossimo prezzo. La funzione di attivazione è disattivata nello strato di output (OAF=0).

Input dell'indicatore:

extern int lastBar - Ultimo bar nei dati passati
extern int futBars - # di future barre da prevedere
extern int numLayers - # di strati inclusi input, nascosti e output (2..6)
extern int numInputs - # di input
extern int numNeurons1 - # di neuroni nel primo strato nascosto o di output
extern int numNeurons2 - # di neuroni nel secondo strato nascosto o di output
extern int numNeurons3 - # di neuroni nel terzo strato nascosto o di output
extern int numNeurons4 - # di neuroni nel quarto strato nascosto o di output
extern int numNeurons5 - # di neuroni nel quinto strato nascosto o di output
extern int ntr - # di set di addestramento
extern int nep - Max # di epoche
extern int maxMSEpwr - imposta maxMSE=10^maxMSEpwr; l'addestramento si ferma < maxMSE
extern int AFT - Tipo di funzione di attivazione (0:sigm, 1:tanh, 2:x/(1+x))

L'indicatore traccia tre curve sul grafico:

colore rosso - previsioni dei futuri prezzi
colore nero - prezzi di apertura passati, utilizzati come output attesi per la rete
colore blu - output della rete per gli input di addestramento

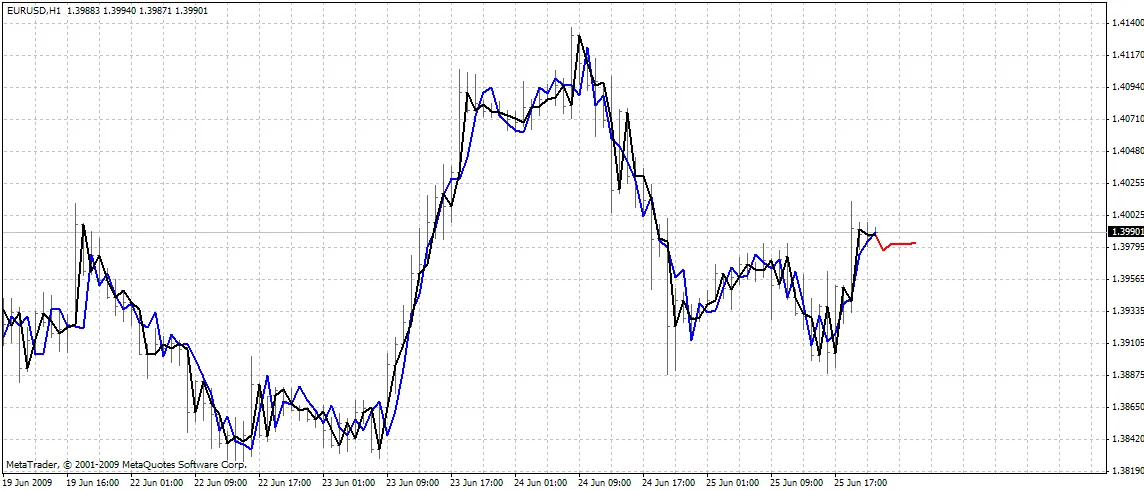
BPNN Predictor.mq4 - prevede i futuri prezzi di apertura smussati. Utilizza la smussatura EMA con periodo smoothPer.

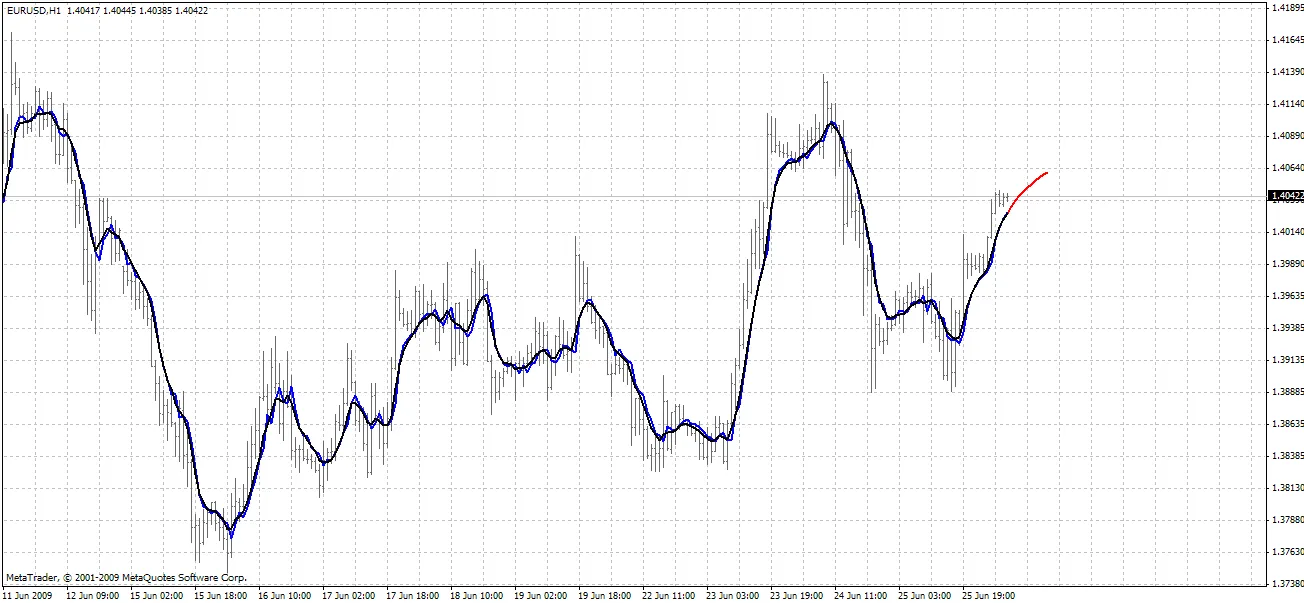
Impostazione iniziale:

Copiare BPNN.DLL nella cartella C:\Program Files\MetaTrader 4\experts\libraries
In MetaTrader: Strumenti - Opzioni - Expert Advisors - Consenti importazioni DLL

È anche possibile compilare il proprio file DLL utilizzando i codici sorgente in BPNN.zip.

Raccomandazioni:

Una rete con tre strati (numLayers=3: uno di input, uno nascosto e uno di output) è sufficiente per la maggior parte dei casi. Secondo il Teorema di Cybenko (1989), una rete con uno strato nascosto è in grado di approssimare qualsiasi funzione continua multivariata con il grado di accuratezza desiderato; una rete con due strati nascosti è in grado di approssimare qualsiasi funzione multivariata discontinua:
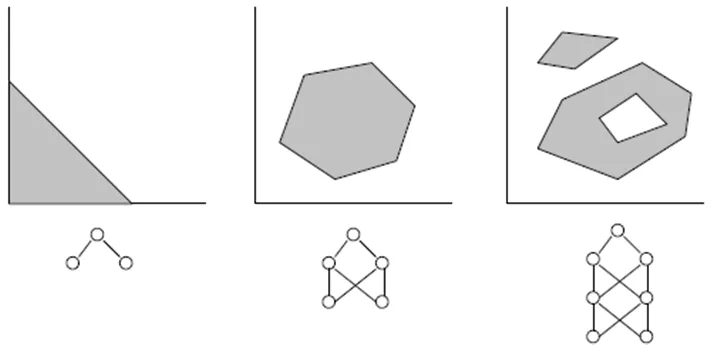
Il numero ottimale di neuroni nello strato nascosto può essere trovato tramite tentativi ed errori. Le seguenti "regole empiriche" possono essere trovate in letteratura: # di neuroni nascosti = (# di input + # di output)/2, o SQRT(# di input * # di output). Tieni traccia dell'errore di addestramento, riportato dall'indicatore nella finestra degli esperti di MetaTrader.
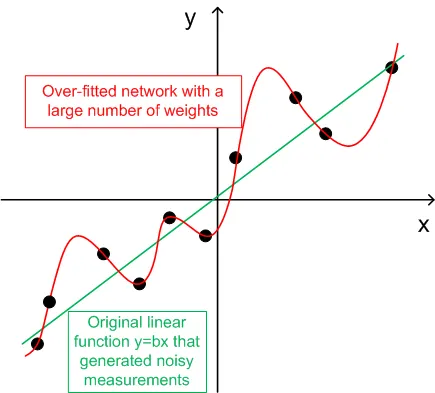
Per la generalizzazione, il numero di set di addestramento (ntr) dovrebbe essere scelto da 2 a 5 volte il numero totale dei pesi nella rete. Ad esempio, per impostazione predefinita, BPNN Predictor.mq4 utilizza una rete 12-5-1. Il numero totale di pesi è (12+1)*5+6=71. Pertanto, il numero di set di addestramento (ntr) dovrebbe essere almeno 142. Il concetto di generalizzazione e memorizzazione (over-fitting) è spiegato nel grafico qui sotto.
I dati di input per la rete dovrebbero essere trasformati in stazionari. I prezzi Forex non sono stazionari. È anche consigliabile normalizzare gli input nell'intervallo -1..+1.

Il grafico qui sotto mostra una funzione lineare y=b*x (x-input, y-output) i cui output sono corrotti da rumore. Questo rumore aggiunto causa la deviazione degli output misurati (punti neri) da una retta. La funzione y=f(x) può essere modellata da una rete neurale feed forward. La rete con un gran numero di pesi può adattarsi ai dati misurati con zero errore. Il suo comportamento è mostrato come la curva rossa che passa attraverso tutti i punti neri. Tuttavia, questa curva rossa non ha niente a che fare con la funzione lineare originale y=b*x (verde). Quando questa rete over-fittata viene utilizzata per prevedere i valori futuri della funzione y(x), porterà a grandi errori a causa della casualità del rumore aggiunto.

In cambio della condivisione di questi codici, l'autore ha una piccola richiesta. Se sei riuscito a creare un sistema di trading redditizio basato su questi codici, ti prego di condividere la tua idea con me inviando un'email direttamente a vlad1004@yahoo.com.

Buona fortuna!

Previsione dei Prezzi con Reti Neurali: Un Guida per Trader

Esempi di utilizzo della libreria NN:

Post correlati