Predicción de Precios en Trading con Redes Neuronales

Autor: gpwr

Historial de Versiones:

26/06/2009: Se añadió un nuevo indicador BPNN Predictor con Suavizado.mq4, en el que los precios se suavizan usando EMA antes de realizar las predicciones.
20/08/2009: Se corrigió el código que calcula la función de activación de las neuronas para evitar excepciones aritméticas; se actualizó BPNN.cpp y BPNN.dll.
21/08/2009: Se añadió la limpieza de memoria al final de la ejecución de la DLL; se actualizó BPNN.cpp y BPNN.dll.

Breve Teoría de las Redes Neuronales:

Una red neuronal es un modelo ajustable de salidas como funciones de entradas. Está compuesta por varias capas:

capa de entrada, que consiste en los datos de entrada
capa oculta, que se compone de nodos de procesamiento llamados neuronas
capa de salida, que consiste en una o varias neuronas, cuyas salidas son las salidas de la red.

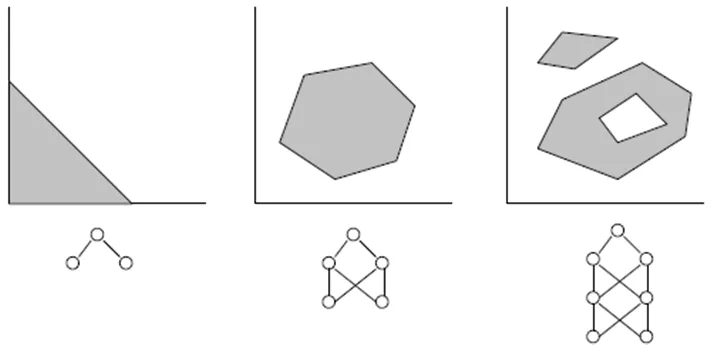
Todos los nodos de capas adyacentes están interconectados. Estas conexiones se llaman sinapsis. Cada sinapsis tiene un coeficiente de escalado asignado, por el cual los datos propagados a través de la sinapsis se multiplican. Estos coeficientes de escalado se denominan pesos (w[i][j][k]). En una Red Neuronal de Propagación Adelante (FFNN), los datos se propagan de las entradas a las salidas. Aquí hay un ejemplo de FFNN con una capa de entrada, una capa de salida y dos capas ocultas:

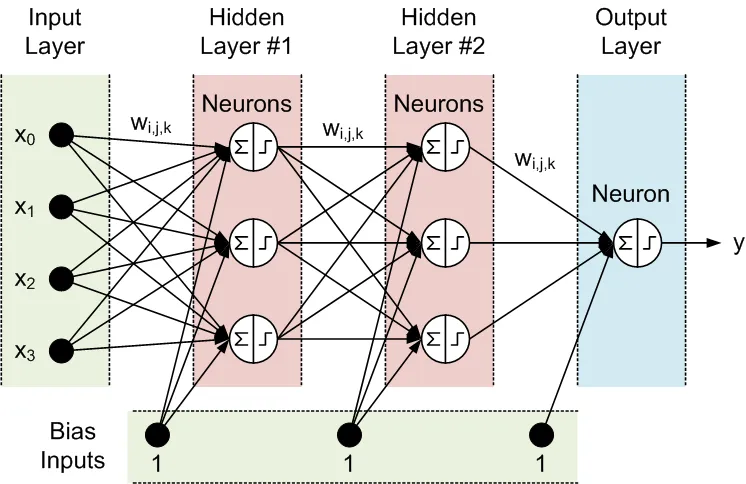
La topología de una FFNN a menudo se abrevia de la siguiente manera: <número de entradas> - <número de neuronas en la primera capa oculta> - <número de neuronas en la segunda capa oculta> -...- <número de salidas>. La red anterior puede ser referida como una red 4-3-3-1.

Los datos son procesados por las neuronas en dos pasos, que se muestran dentro del círculo con un signo de suma y un signo de paso:

Todos los inputs se multiplican por los pesos asociados y se suman
Las sumas resultantes son procesadas por la función de activación de la neurona, cuya salida es la salida de la neurona.

Es la función de activación de la neurona la que aporta no linealidad al modelo de red neuronal. Sin ella, no hay razón para tener capas ocultas, y la red neuronal se convierte en un modelo autorregresivo lineal (AR).

Los archivos de biblioteca incluidos para funciones NN permiten seleccionar entre tres funciones de activación:

sigmoide: sigm(x)=1/(1+exp(-x)) (#0)
tangente hiperbólica: tanh(x)=(1-exp(-2x))/(1+exp(-2x)) (#1)
función racional: x/(1+|x|) (#2)

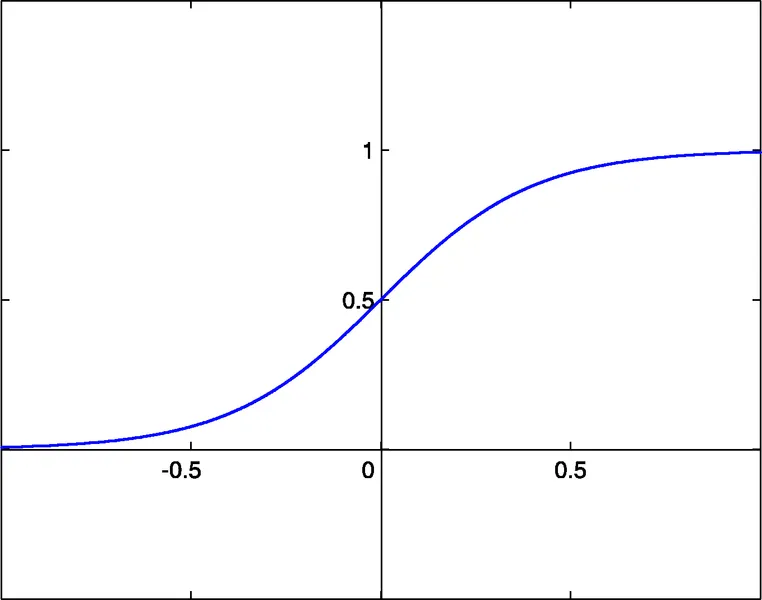
El umbral de activación de estas funciones es x=0. Este umbral puede ser movido a lo largo del eje x gracias a una entrada adicional de cada neurona, llamada entrada de sesgo, que también tiene un peso asignado.

El número de entradas, salidas, capas ocultas, neuronas en estas capas y los valores de los pesos de sinapsis describen completamente una FFNN, es decir, el modelo no lineal que crea. Para encontrar los pesos, la red debe ser entrenada. Durante un entrenamiento supervisado, se alimentan a la red varios conjuntos de entradas pasadas y las correspondientes salidas esperadas. Los pesos se optimizan para lograr el menor error entre las salidas de la red y las salidas esperadas. El método más simple de optimización de pesos es la retropropagación de errores, que es un método de descenso de gradiente. La función de entrenamiento Train() utiliza una variante de este método, denominada Retropropagación Mejorada Plus (iRProp+). Este método se describe aquí:

http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.17.1332

La principal desventaja de los métodos de optimización basados en gradientes es que a menudo encuentran un mínimo local. Para series caóticas como las series de precios, la superficie de error de entrenamiento tiene una forma muy compleja con muchos mínimos locales. Para tales series, un algoritmo genético es un método de entrenamiento preferido.

Archivos incluidos:

BPNN.dll - archivo de biblioteca
BPNN.zip - archivo comprimido de todos los archivos necesarios para compilar BPNN.dll en C++
BPNN Predictor.mq4 - indicador que predice los precios de apertura futuros
BPNN Predictor con Suavizado.mq4 - indicador que predice precios de apertura suavizados

El archivo BPNN.cpp tiene dos funciones: Train() y Test(). Train() se utiliza para entrenar la red basada en los valores de entrada y salida esperados proporcionados. Test() se usa para calcular las salidas de la red utilizando los pesos optimizados que se encontraron mediante Train().

Aquí está la lista de parámetros de entrada (verde) y salida (azul) de Train():

double inpTrain[] - Datos de entrada para el entrenamiento (arreglo 1D que lleva datos 2D, el más antiguo primero)
double outTarget[] - Datos de salida objetivo para entrenamiento (datos 2D como arreglo 1D, el más antiguo primero)
double outTrain[] - Arreglo de salida 1D para contener las salidas de la red del entrenamiento
int ntr - Número de conjuntos de entrenamiento
int UEW - Usar pesos externos para la inicialización (1=usar extInitWt, 0=usar aleatorio)
double extInitWt[] - Arreglo de entrada 1D para contener un arreglo 3D de pesos externos iniciales
double trainedWt[] - Arreglo de salida 1D para contener un arreglo 3D de pesos entrenados
int numLayers - Número de capas incluyendo entrada, ocultas y salida
int lSz[] - Número de neuronas en capas. lSz[0] es el número de entradas de la red
int AFT - Tipo de función de activación de neuronas (0:sigm, 1:tanh, 2:x/(1+x))
int OAF - 1 habilita función de activación para la capa de salida; 0 desactiva
int nep - Número máximo de épocas de entrenamiento
double maxMSE - MSE máximo; el entrenamiento se detiene una vez alcanzado el maxMSE

Aquí está la lista de parámetros de entrada (verde) y salida (azul) de Test():

double inpTest[] - Datos de prueba de entrada (datos 2D como arreglo 1D, el más antiguo primero)
double outTest[] - Arreglo de salida 1D para contener las salidas de la red del entrenamiento (el más antiguo primero)
int ntt - Número de conjuntos de prueba
double extInitWt[] - Arreglo de entrada 1D para contener un arreglo 3D de pesos externos iniciales
int numLayers - Número de capas incluyendo entrada, ocultas y salida
int lSz[] - Número de neuronas en capas. lSz[0] es el número de entradas de la red
int AFT - Tipo de función de activación de neuronas (0:sigm, 1:tanh, 2:x/(1+x))
int OAF - 1 habilita función de activación para la capa de salida; 0 desactiva

Si se debe usar la función de activación en la capa de salida o no (valor del parámetro OAF) depende de la naturaleza de las salidas. Si las salidas son binarias, que a menudo es el caso en problemas de clasificación, entonces se debe usar la función de activación en la capa de salida (OAF=1). Por favor, ten en cuenta que la función de activación #0 (sigmoide) tiene niveles saturados en 0 y 1, mientras que las funciones de activación #1 y #2 tienen niveles de -1 y 1. Si la salida de la red es una predicción de precios, entonces no se necesita una función de activación en la capa de salida (OAF=0).

Ejemplos de uso de la biblioteca NN:

BPNN Predictor.mq4 - predice los precios de apertura futuros. Las entradas de la red son cambios relativos de precios:

x[i]=Open[test_bar]/Open[test_bar+delay[i]]-1.0

donde delay[i] se calcula como un número de Fibonacci (1,2,3,5,8,13,21..). La salida de la red es el cambio relativo predicho del siguiente precio. La función de activación se desactiva en la capa de salida (OAF=0).

Entradas del indicador:

extern int lastBar - Última barra en los datos pasados
extern int futBars - Número de barras futuras a predecir
extern int numLayers - Número de capas incluyendo entrada, ocultas y salida (2..6)
extern int numInputs - Número de entradas
extern int numNeurons1 - Número de neuronas en la primera capa oculta o de salida
extern int numNeurons2 - Número de neuronas en la segunda capa oculta o de salida
extern int numNeurons3 - Número de neuronas en la tercera capa oculta o de salida
extern int numNeurons4 - Número de neuronas en la cuarta capa oculta o de salida
extern int numNeurons5 - Número de neuronas en la quinta capa oculta o de salida
extern int ntr - Número de conjuntos de entrenamiento
extern int nep - Número máximo de épocas
extern int maxMSEpwr - establece maxMSE=10^maxMSEpwr; el entrenamiento se detiene < maxMSE
extern int AFT - Tipo de función de activación (0:sigm, 1:tanh, 2:x/(1+x))

El indicador traza tres curvas en el gráfico:

color rojo - predicciones de precios futuros
color negro - precios de apertura de entrenamiento pasados, que se utilizaron como salidas esperadas para la red
color azul - salidas de la red para las entradas de entrenamiento

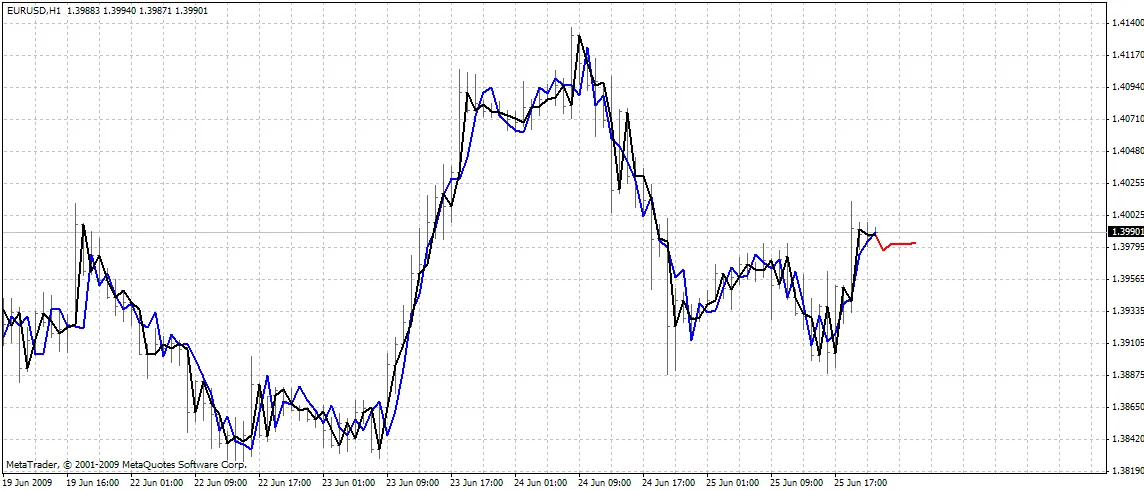
BPNN Predictor.mq4 - predice los precios de apertura suavizados futuros. Utiliza suavizado EMA con periodo smoothPer.

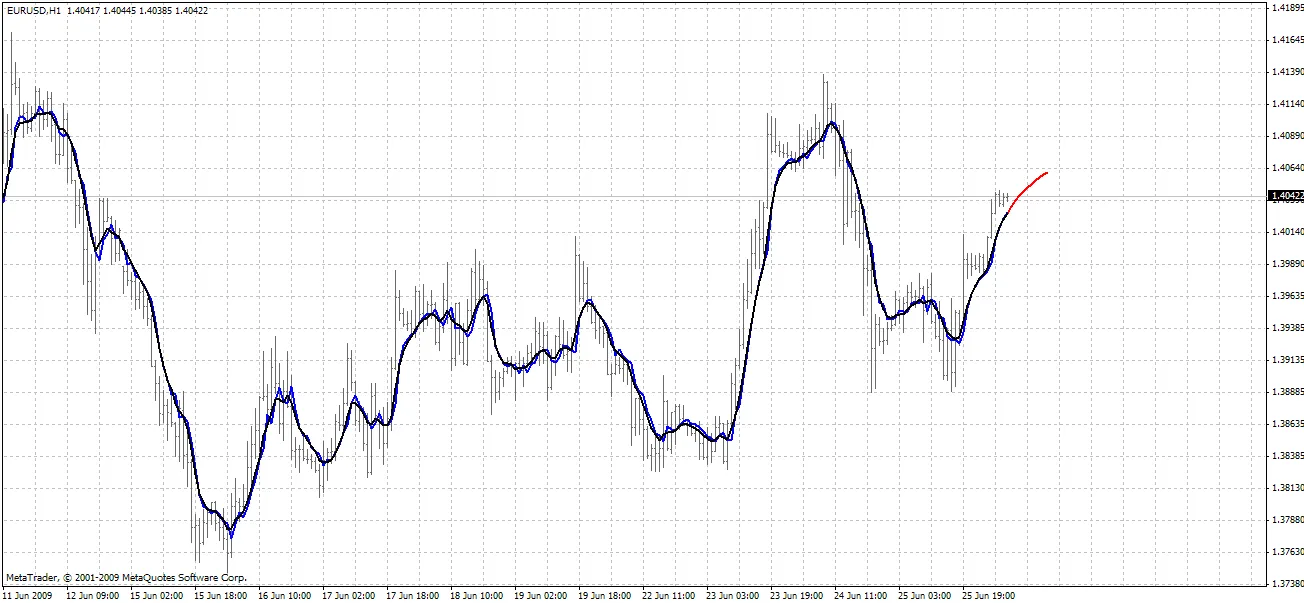
Configuración Inicial:

Copie el archivo BPNN.DLL en C:\Program Files\MetaTrader 4\experts\libraries
En MetaTrader: Herramientas - Opciones - Asesores Expertos - Permitir importaciones DLL

También puede compilar su propio archivo DLL utilizando los códigos fuente en BPNN.zip.

Recomendaciones:

Una red con tres capas (numLayers=3: una de entrada, una oculta y una de salida) es suficiente para la gran mayoría de los casos. Según el Teorema de Cybenko (1989), una red con una capa oculta es capaz de aproximar cualquier función continua multivariante a cualquier grado de precisión deseado; una red con dos capas ocultas es capaz de aproximar cualquier función multivariante discontinua.
El número óptimo de neuronas en la capa oculta se puede encontrar mediante prueba y error. Se pueden encontrar las siguientes "reglas prácticas" en la literatura: número de neuronas ocultas = (número de entradas + número de salidas) / 2, o SQRT(número de entradas * número de salidas). Mantenga un seguimiento del error de entrenamiento, que es informado por el indicador en la ventana de expertos de MetaTrader.
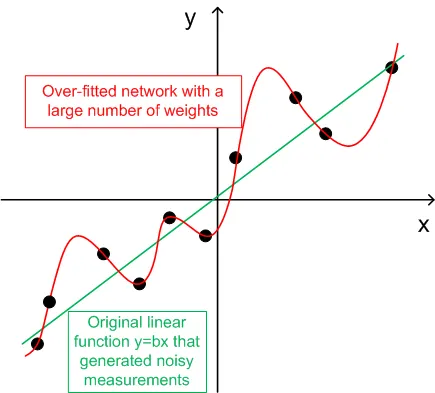
Para generalización, el número de conjuntos de entrenamiento (ntr) debe ser elegido de 2 a 5 veces el número total de pesos en la red. Por ejemplo, por defecto, BPNN Predictor.mq4 utiliza una red 12-5-1. El número total de pesos es (12+1)*5+6=71. Por lo tanto, el número de conjuntos de entrenamiento (ntr) debe ser al menos 142. El concepto de generalización y memorización (sobreajuste) se explica en el gráfico a continuación.
Los datos de entrada a la red deben transformarse a estacionarios. Los precios del Forex no son estacionarios. También se recomienda normalizar las entradas al rango de -1..+1.

El gráfico a continuación muestra una función lineal y=x (x-entrada, y-salida) cuyas salidas están contaminadas por ruido. Este ruido añadido hace que las salidas de la función medida (puntos negros) se desvíen de una línea recta. La función y=f(x) puede ser modelada por una red neuronal de propagación hacia adelante. La red con un gran número de pesos puede ajustarse a los datos medidos con un error cero. Su comportamiento se muestra como la curva roja que pasa por todos los puntos negros. Sin embargo, esta curva roja no tiene nada que ver con la función lineal original y=x (verde). Cuando esta red sobreajustada se utiliza para predecir valores futuros de la función y(x), resultará en grandes errores debido a la aleatoriedad del ruido añadido.

Como intercambio por compartir estos códigos, el autor tiene un pequeño favor que pedir. Si lograste crear un sistema de trading rentable basado en estos códigos, por favor comparte tu idea conmigo enviando un correo electrónico directamente a vlad1004@yahoo.com.

¡Buena suerte!

Predicción de Precios en Trading con Redes Neuronales

Ejemplos de uso de la biblioteca NN:

Publicaciones relacionadas