Hodrick-Prescott Filter: Ein Leitfaden für Trader

Autor: gpwr

Ein besonderes Merkmal des Hodrick-Prescott-Filters ist, dass er keine Verzögerung aufweist. Er wird berechnet, indem die Zielfunktion minimiert wird:

F = Sum((y[i] - x[i])^2,i=0..n-1) + lambda*Sum((y[i+1]+y[i-1]-2*y[i])^2,i=1..n-2)

Hierbei ist x[] der Preis und y[] die Filterwerte. Im Folgenden sehen wir ein Beispiel für das Verhalten des Filters (siehe die angehängte Datei HP.mq4):

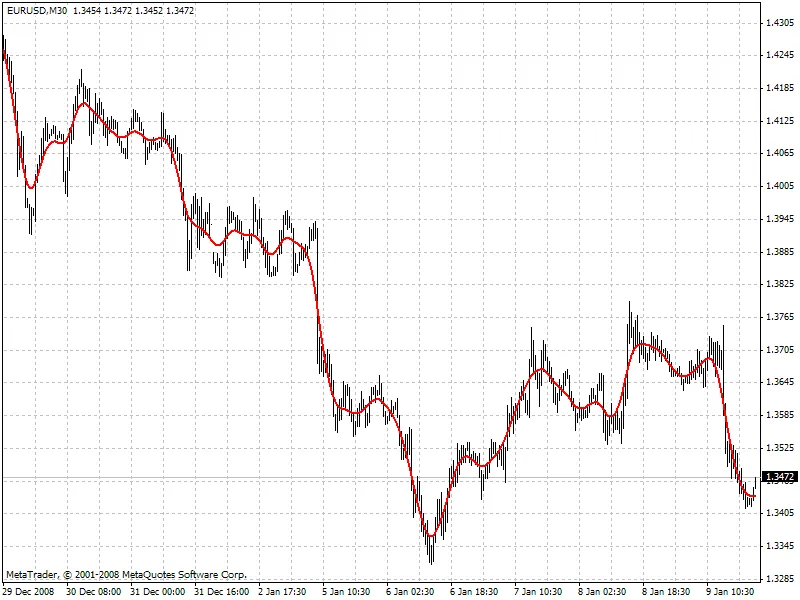
Wenn der Hodrick-Prescott-Filter die Zukunft „sieht“, welche zukünftigen Werte schlägt er dann vor? Um diese Frage zu beantworten, sollten wir einen digitalen Tiefpassfilter finden, dessen Frequenzparameter ähnlich dem des Hodrick-Prescott-Filters ist, jedoch mit Werten, die direkt aus den vergangenen Werten des „Zwillingsfilters“ berechnet werden, d.h.

y[i] = Sum(a[k]*x[i-k],k=0..nx-1) - FIR-Filter

oder

y[i] = Sum(a[k]*x[i-k],k=0..nx-1) + Sum(b[k]*y[i-k],k=1..ny) - IIR-Filter

Es ist besser, den „Zwillingsfilter“ mit einer frequenzunabhängigen Verzögerung Тdel (konstante Gruppenverzögerung) auszuwählen. IIR-Filter sind nicht geeignet. Für FIR-Filter gilt die Bedingung für eine frequenzunabhängige Verzögerung:

a[i] = +/-a[nx-1-i], i = 0..nx-1

Der einfachste FIR-Filter mit konstanter Verzögerung ist der Simple Moving Average (SMA):

y[i] = Sum(x[i-k],k=0..nx-1)/nx

Wenn nx eine ungerade Zahl ist, gilt Тdel = (nx-1)/2. Wenn wir die Werte des SMA-Filters um die Anzahl der Balken, die Тdel entspricht, in die Vergangenheit verschieben, stimmen die SMA-Werte mit den Werten des Hodrick-Prescott-Filters überein. Die exakte Mathematik kann aufgrund der erheblichen Unterschiede in den Frequenzparametern der beiden Filter nicht erreicht werden (siehe das folgende Diagramm):

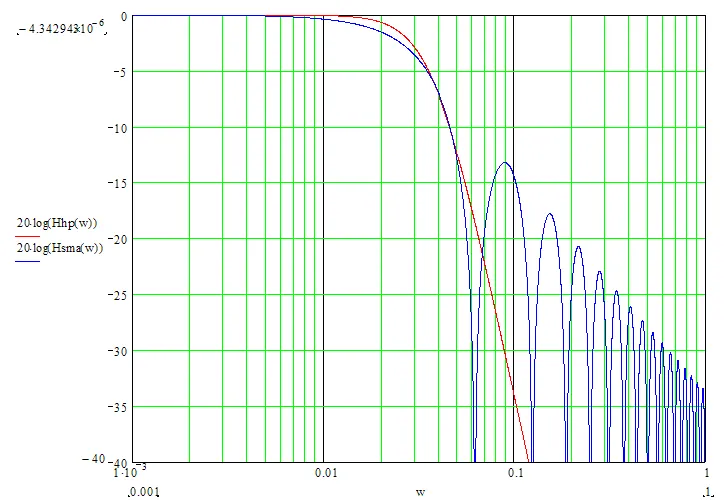
Um die bestmögliche Übereinstimmung zwischen den Filterwerten zu erreichen, empfehle ich, dass ihre Kanalbreiten ähnlich sind (zum Beispiel -6dB). Die Kanalbreite von -6dB für den Hodrick-Prescott-Filter wird wie folgt berechnet:

wc = 2*arcsin(0.5/lambda^0.25).

Die Kanalbreite von -6dB für den SMA-Filter wird durch numerische Berechnung über die folgende Gleichung ermittelt:

|H(w)| = sin(nx*wc/2)/sin(wc/2)/nx = 0.5

Das folgende Diagramm vergleicht die Werte der beiden Filter mit ähnlicher Kanalbreite: rot - Hodrick-Prescott-Filter (FiltPer = 25), blau - SMA (Period = 15, Shift = -7). Beachte, dass es für die letzten 7 Balken keine SMA-Daten gibt, da er zukünftige Preise kennen muss. Im Gegensatz dazu zeigt der Hodrick-Prescott-Filter (rot) einige Werte. Wenn der verschobene SMA die Werte des Hodrick-Prescott-Filters in den letzten 7 Balken nach dem Erscheinen der zukünftigen Preise wiederholt, was könnten diese Werte dann sein?

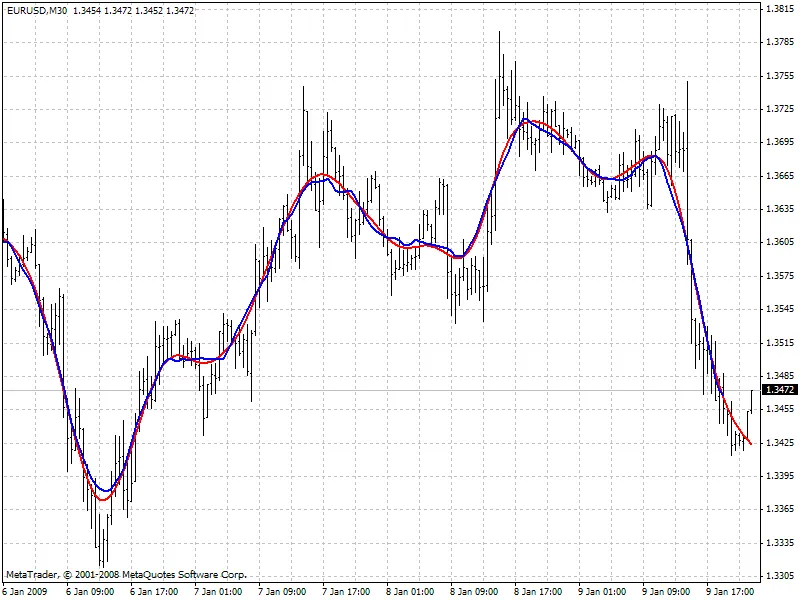
Vorhersagealgorithmen:

Der Indikator bietet zwei Vorhersagemethoden:

Methode 1:

• Setze die SMA-Länge auf 3 und verschiebe sie um 1 Balken in die Vergangenheit. Mit dieser Länge existiert der verschobene SMA nur für den letzten Balken (Bar = 0), da er den Wert des nächsten zukünftigen Preises Close[-1] benötigt.
• Berechne die Kanalbreite des SMA-Filters. Setze sie gleich der des Hodrick-Prescott-Filters. Finde lambda.
• Berechne den Hodrick-Prescott-Filterwert am letzten Balken HP[0] und gehe davon aus, dass SMA[0] mit unbekanntem Close[-1] den gleichen Wert liefert.
• Finde Close[-1] = 3*HP[0] - Close[0] - Close[1]
• Erhöhe die Länge des SMA auf 5. Wiederhole die Berechnungen und finde Close[-2] = 5*HP[0] - Close[-1] - Close[0] - Close[1] - Close[2]. Setze dies fort, bis die angegebene Anzahl zukünftiger FutBars-Preise berechnet ist.

Methode 2:

• Setze die SMA-Länge auf 2*FutBars+1 und verschiebe den SMA um FutBars in die Vergangenheit.
• Berechne die Kanalbreite des SMA-Filters. Setze sie gleich der des Hodrick-Prescott-Filters. Finde lambda.
• Berechne die Hodrick-Prescott-Filterwerte an den letzten FutBars und gehe davon aus, dass der SMA sich ähnlich verhält, wenn neue Preise erscheinen.
• Finde Close[-1] = (2*FutBars+1)*HP[FutBars-1] - Sum(Close[i],i=0..2*FutBars-1), Close[-2] = (2*FutBars+1)*HP[FutBars-2] - Sum(Close[i],i=-1..2*FutBars-2), etc.

Der Indikator bietet folgende Eingaben:

• Methode - Vorhersagemethode
• LastBar - Anzahl des letzten Balkens, um Vorhersagen auf den vorhandenen Preisen zu überprüfen (LastBar >= 0)
• PastBars - Anzahl der vorherigen Balken, für die der Hodrick-Prescott-Filter berechnet wird (je mehr, desto besser oder mindestens PastBars > 2*FutBars)
• FutBars - Anzahl der vorhergesagten zukünftigen Werte

Der Indikator hebt die vorhergesagten Werte in Rot hervor. Methode 1 wird im folgenden Beispiel verwendet:

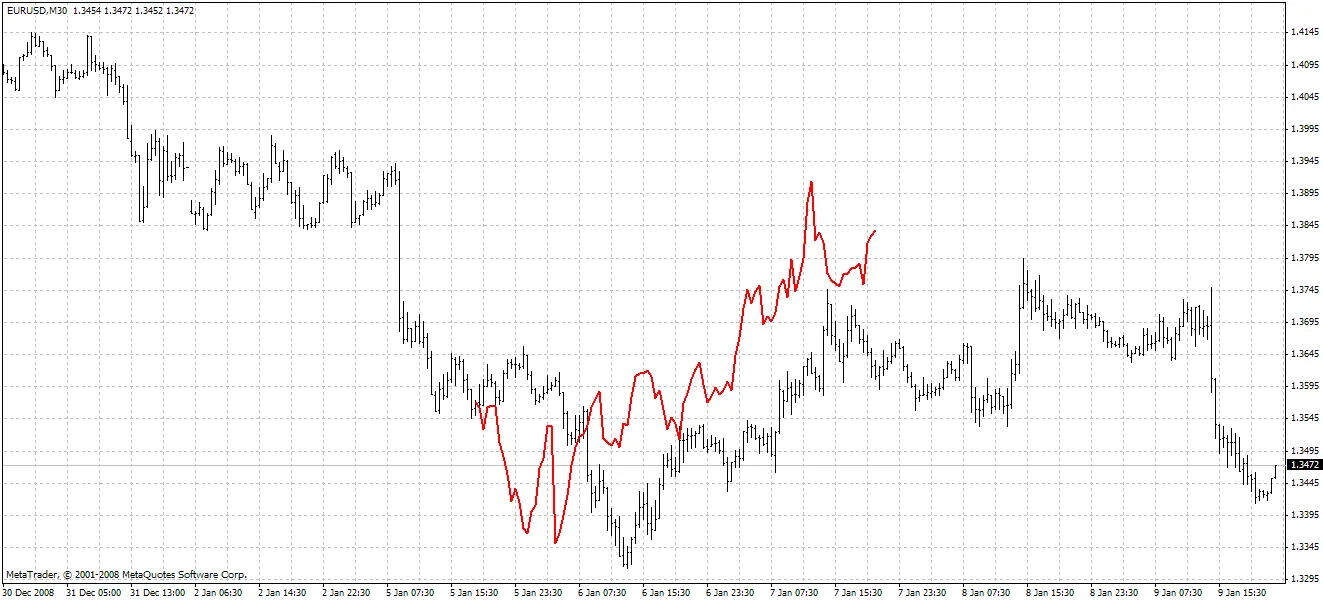
Methode 2:

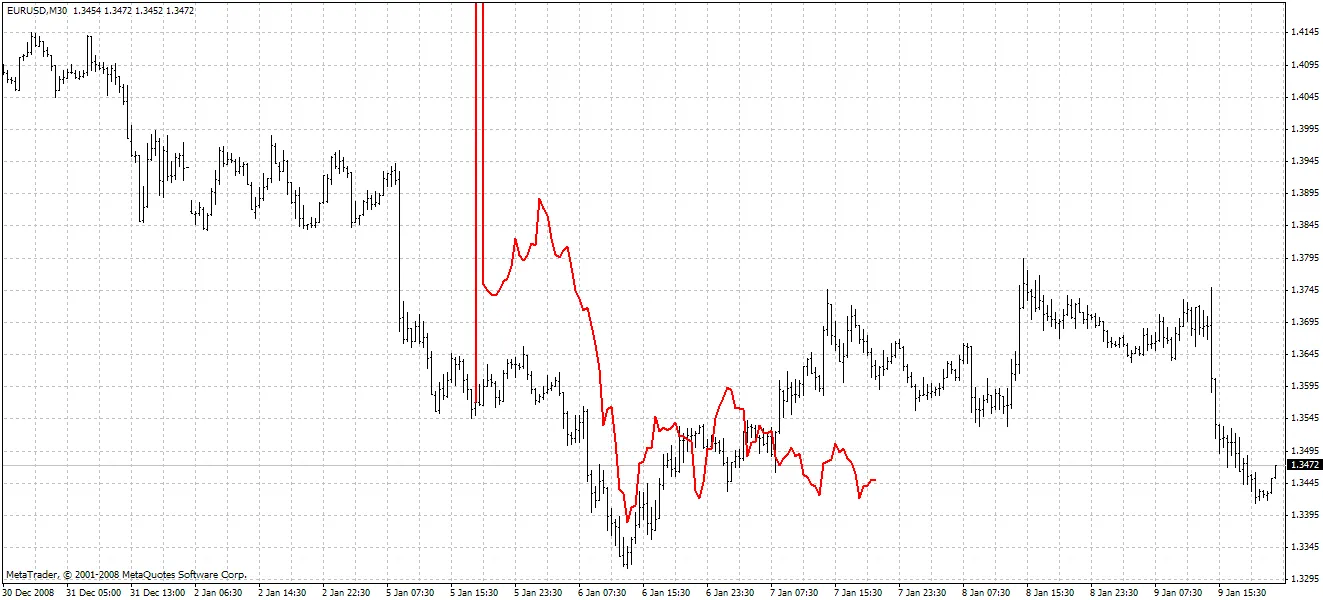
Die zweite Methode ist genauer, weist jedoch häufig große Spitzen beim ersten vorhergesagten Preis auf. Die beschriebene Vorhersagemethode kann verbessert werden, indem nach einem FIR-Filter mit dem Frequenzparameter gesucht wird, der näher am Hodrick-Prescott-Filter liegt. Beispielsweise können Sie Hanning-, Blackman-, Kaiser- und andere Filter mit konstanter Verzögerung anstelle des SMA ausprobieren.

Der Autor dankt dem Benutzer Korey für den ursprünglichen Hodrick-Prescott-Filterindikator, der im folgenden Forum-Abschnitt veröffentlicht wurde (auf Russisch):

https://www.mql5.com/ru/forum/113677/page2