Entendendo o Filtro Hodrick-Prescott: Previsões e Aplicações no Trading

Autor: gpwr

Uma das características marcantes do filtro Hodrick-Prescott é a sua capacidade de não apresentar atrasos. Esse filtro é calculado ao minimizar a função objetivo:

F = Soma((y[i] - x[i])^2,i=0..n-1) + lambda*Soma((y[i+1]+y[i-1]-2*y[i])^2,i=1..n-2)

onde x[] representa os preços e y[] os valores filtrados. Abaixo está um exemplo do comportamento do filtro (veja o arquivo HP.mq4 anexado).

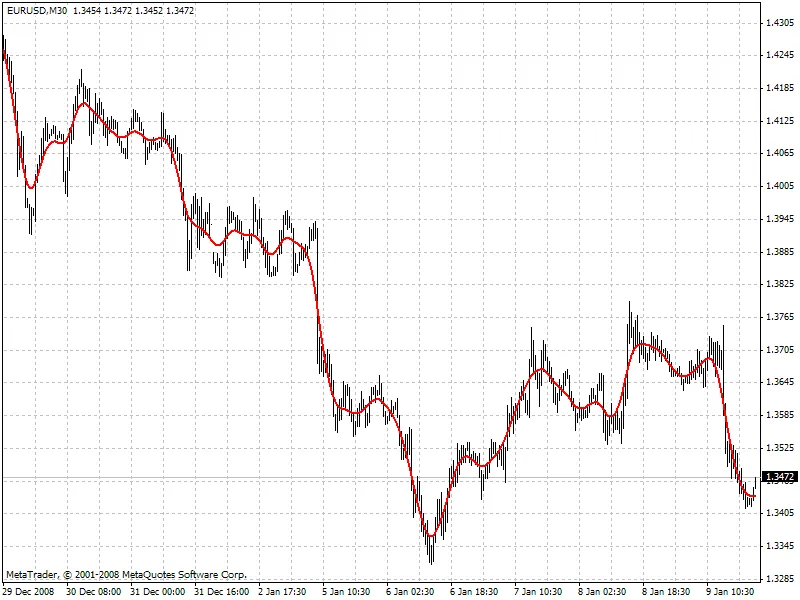
Se o filtro Hodrick-Prescott antecipa o futuro, quais valores futuros ele sugere? Para responder a essa pergunta, precisamos encontrar um filtro digital de baixa frequência com um parâmetro de frequência semelhante ao do filtro Hodrick-Prescott, mas com valores calculados diretamente usando os valores passados do "filtro gêmeo", ou seja:

y[i] = Soma(a[k]*x[i-k],k=0..nx-1) - filtro FIR

ou

y[i] = Soma(a[k]*x[i-k],k=0..nx-1) + Soma(b[k]*y[i-k],k=1..ny) - filtro IIR

É preferível selecionar o "filtro gêmeo" com um atraso Tdel independente da frequência (atraso de grupo constante). Filtros IIR não são adequados. Para filtros FIR, a condição para um atraso independente da frequência é:

a[i] = +/-a[nx-1-i], i = 0..nx-1

O filtro FIR mais simples com atraso constante é a Média Móvel Simples (SMA):

y[i] = Soma(x[i-k],k=0..nx-1)/nx

No caso de nx ser um número ímpar, Tdel = (nx-1)/2. Se deslocarmos os valores do filtro SMA para o passado pelo número de barras igual a Tdel, os valores do SMA coincidem com os do filtro Hodrick-Prescott. A matemática exata não pode ser alcançada devido às diferenças significativas nos parâmetros de frequência dos dois filtros (veja o gráfico abaixo):

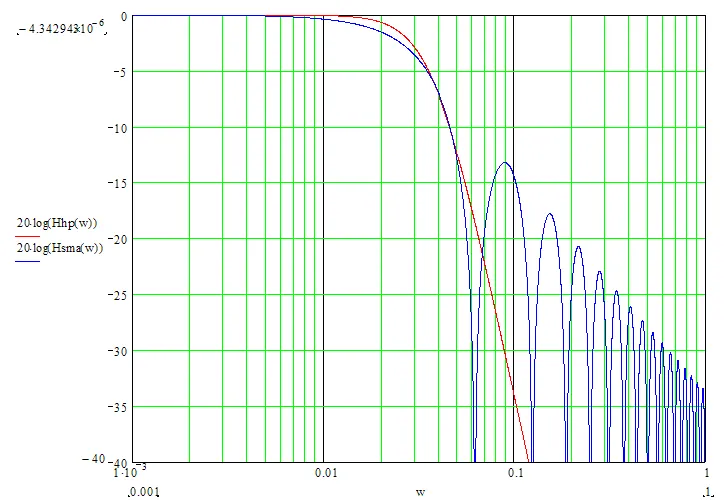
Para alcançar a melhor correspondência entre os valores dos filtros, recomendo que as larguras de canal sejam semelhantes (por exemplo, -6dB). A largura de canal do filtro Hodrick-Prescott de -6dB é calculada da seguinte forma:

wc = 2*arcsin(0.5/lambda^0.25).

A largura de canal de -6dB para o filtro SMA é calculada por computação numérica através da seguinte equação:

|H(w)| = sin(nx*wc/2)/sin(wc/2)/nx = 0.5

O gráfico abaixo compara os valores de dois filtros com largura de canal semelhante: em vermelho - filtro Hodrick-Prescott (FiltPer = 25), em azul - SMA (Período = 15, Atraso = -7). Note que não há dados SMA para as últimas 7 barras, pois ele precisa conhecer os preços futuros. Por outro lado, o filtro Hodrick-Prescott (vermelho) apresenta alguns valores. Se o SMA deslocado repetir os valores do filtro Hodrick-Prescott nas últimas 7 barras após o aparecimento dos preços futuros, quais podem ser esses valores?

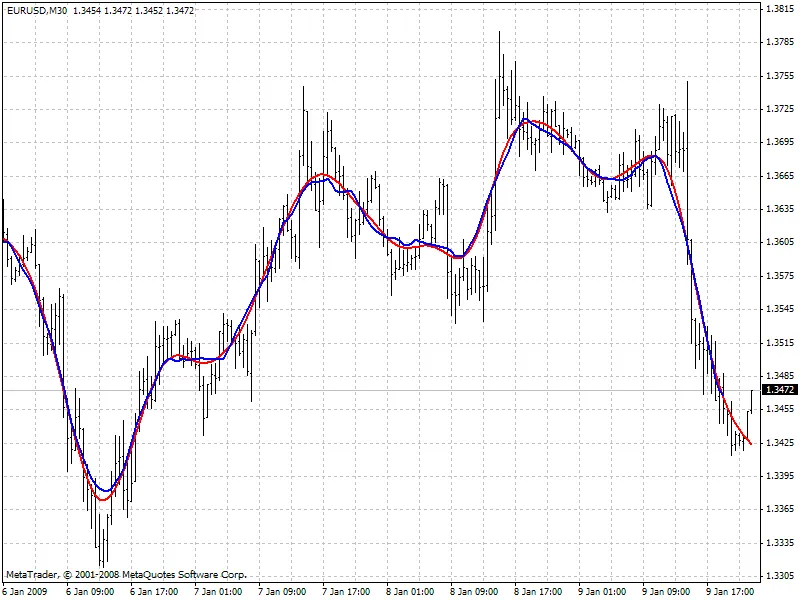
Algoritmos de Previsão:

O indicador conta com dois métodos de previsão:

Método 1:

• 1. Defina o comprimento da SMA para 3 e desloque-a para o passado em 1 barra. Com esse comprimento, a SMA deslocada não existe apenas para a última barra (Bar = 0), pois precisa do valor do próximo preço futuro Close[-1].
• 2. Calcule a largura de canal do filtro SMA. Iguale-a à do filtro Hodrick-Prescott. Encontre lambda.
• 3. Calcule o valor do filtro Hodrick-Prescott na última barra HP[0] e assuma que SMA[0] com Close[-1] desconhecido dá o mesmo valor.
• 4. Encontre Close[-1] = 3*HP[0] - Close[0] - Close[1]
• 5. Aumente o comprimento da SMA para 5. Repita todos os cálculos e encontre Close[-2] = 5*HP[0] - Close[-1] - Close[0] - Close[1] - Close[2]. Continue até calcular a quantidade especificada de preços futuros FutBars.

Método 2:

• 1. Defina o comprimento da SMA como igual a 2*FutBars+1 e desloque a SMA para o passado em FutBars.
• 2. Calcule a largura de canal do filtro SMA. Iguale-a à do filtro Hodrick-Prescott. Encontre lambda.
• 3. Calcule os valores do filtro Hodrick-Prescott nas últimas FutBars e assuma que a SMA se comporta de forma semelhante quando novos preços aparecem.
• 4. Encontre Close[-1] = (2*FutBars+1)*HP[FutBars-1] - Soma(Close[i],i=0..2*FutBars-1), Close[-2] = (2*FutBars+1)*HP[FutBars-2] - Soma(Close[i],i=-1..2*FutBars-2), etc.

O indicador possui os seguintes inputs:

• Método - método de previsão
• ÚltimaBarra - número da última barra para checar as previsões nos preços existentes (ÚltimaBarra >= 0)
• BarrasPassadas - quantidade de barras anteriores para as quais o filtro Hodrick-Prescott é calculado (quanto mais, melhor, ou pelo menos BarrasPassadas>2*FutBars)
• FutBars - quantidade de valores futuros previstos

O indicador destaca os valores previstos em vermelho. O Método 1 é utilizado no exemplo abaixo:

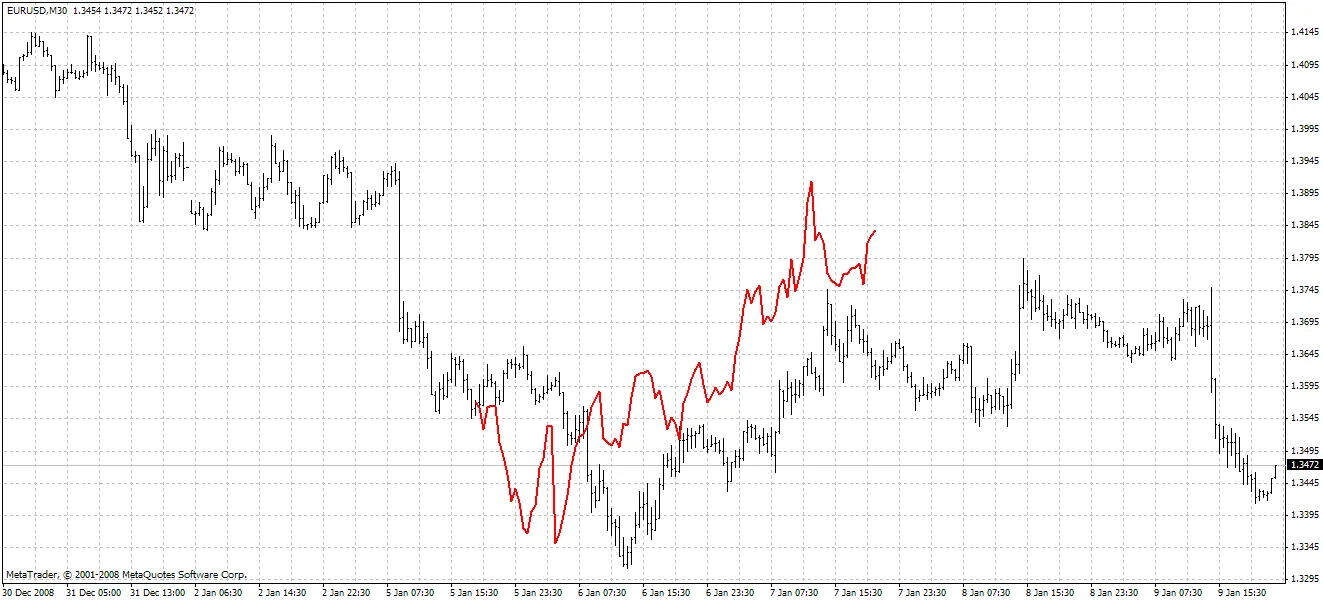
Método 2:

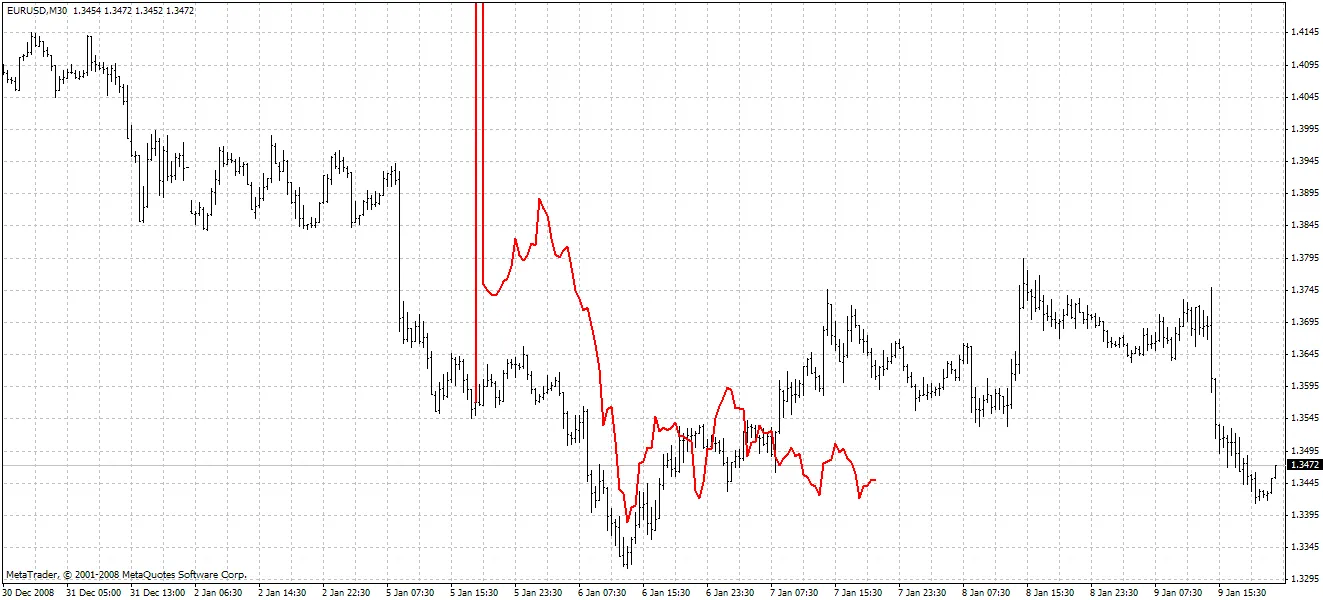
O segundo método é mais preciso, mas muitas vezes apresenta grandes picos no primeiro preço previsto. O método de previsão descrito pode ser melhorado buscando um filtro FIR com o parâmetro de frequência mais próximo do filtro Hodrick-Prescott. Por exemplo, você pode tentar filtros Hanning, Blackman, Kaiser e outros filtros com atraso constante em vez da SMA.

O autor agradece ao usuário Korey pelo indicador original do filtro Hodrick-Prescott postado na seguinte seção do Fórum (em Russo):

https://www.mql5.com/ru/forum/113677/page2