작성자: gpwr
호드릭-프레스콧(Hodrick-Prescott) 필터의 가장 두드러진 특징은 지연이 없다는 점입니다. 이 필터는 목표 함수를 최소화함으로써 계산됩니다.
F = Sum((y[i] - x[i])^2,i=0..n-1) + lambda*Sum((y[i+1]+y[i-1]-2*y[i])^2,i=1..n-2)
여기서 x[]는 가격을, y[]는 필터 값을 나타냅니다. 아래는 필터 작동 방식의 예시입니다 (아래 첨부된 HP.mq4 파일 참조).
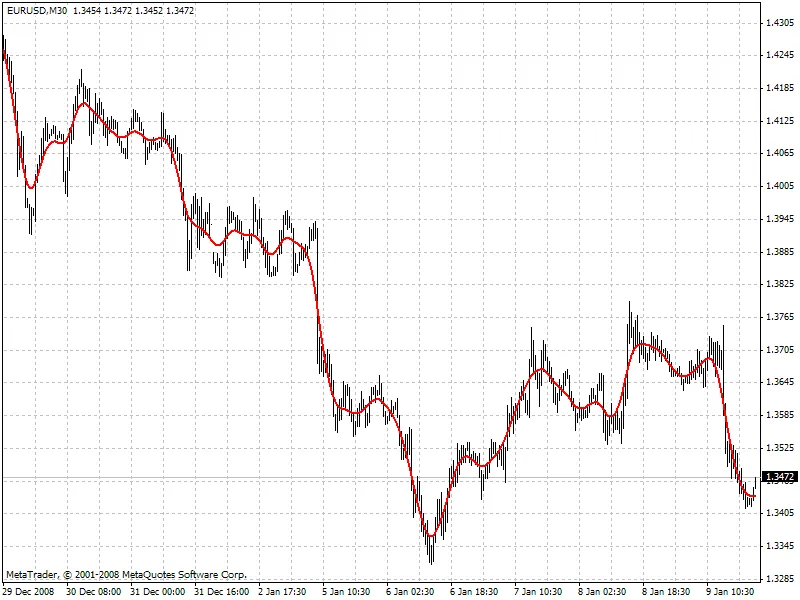
호드릭-프레스콧 필터가 미래를 예측할 수 있다면, 어떤 미래 값을 제시할까요? 이 질문에 대한 답을 찾기 위해서는 호드릭-프레스콧 필터와 유사한 주파수 매개변수를 가진 디지털 저주파 필터를 찾아야 합니다. 즉, "쌍둥이 필터"의 과거 값을 직접 사용하여 계산된 값을 사용해야 합니다.
y[i] = Sum(a[k]*x[i-k],k=0..nx-1) - FIR 필터
또는
y[i] = Sum(a[k]*x[i-k],k=0..nx-1) + Sum(b[k]*y[i-k],k=1..ny) - IIR 필터
주파수 비례 지연 Тdel(상수 그룹 지연)을 가지는 "쌍둥이 필터"를 선택하는 것이 좋습니다. IIR 필터는 적합하지 않습니다. FIR 필터의 경우, 주파수 비례 지연 조건은 다음과 같습니다:
a[i] = +/-a[nx-1-i], i = 0..nx-1
상수 지연을 가지는 가장 간단한 FIR 필터는 단순 이동 평균(SMA)입니다:
y[i] = Sum(x[i-k],k=0..nx-1)/nx
nx가 홀수일 경우, Тdel = (nx-1)/2입니다. SMA 필터의 값을 Тdel만큼 과거로 이동시키면 SMA 값이 호드릭-프레스콧 필터와 일치합니다. 두 필터의 주파수 매개변수 차이로 인해 정확한 수학적 일치는 이루어질 수 없습니다 (아래 차트 참조):
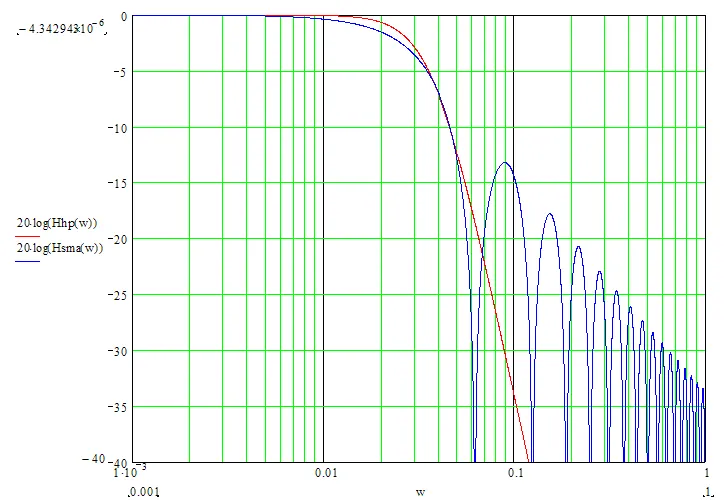
필터 값 간의 가장 가까운 일치를 얻기 위해서는 채널 폭이 유사해야 합니다 (예: -6dB). 호드릭-프레스콧 필터의 -6dB 채널 폭은 다음과 같이 계산됩니다:
wc = 2*arcsin(0.5/lambda^0.25).
-6dB의 SMA 필터 채널 폭은 다음 방정식을 통해 수치 계산으로 구합니다:
|H(w)| = sin(nx*wc/2)/sin(wc/2)/nx = 0.5
아래 차트는 유사한 채널 폭을 가진 두 필터의 값을 비교합니다: 빨간색 - 호드릭-프레스콧 필터 (FiltPer = 25), 파란색 - SMA (Period = 15, Shift = -7). 마지막 7개의 막대에 대해 SMA 데이터는 없습니다. 미래 가격을 알아야 하기 때문입니다. 반면, 호드릭-프레스콧 필터(빨간색)는 몇 가지 값을 보여줍니다. 만약 이동된 SMA가 미래 가격이 나타난 후 마지막 7개의 막대에서 호드릭-프레스콧 필터의 값을 반복한다면, 이 값들은 무엇일까요?
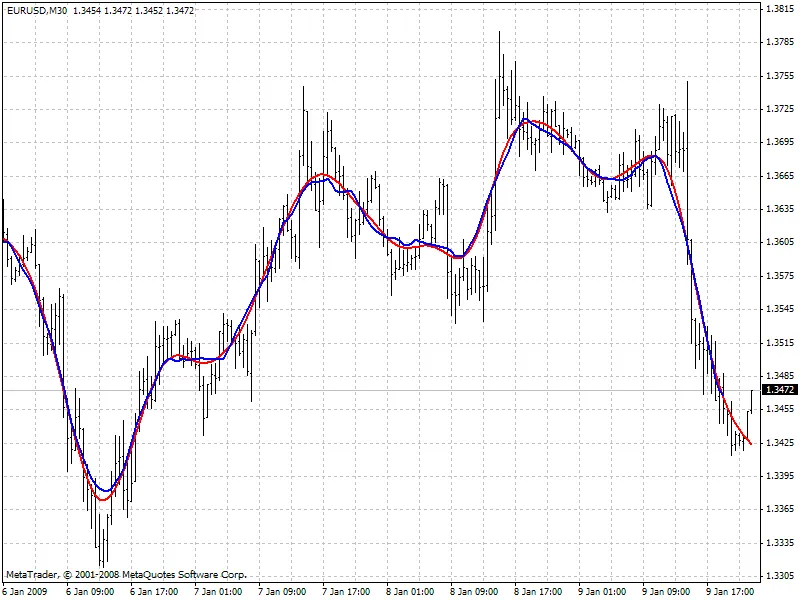
예측 알고리즘:
이 지표는 두 가지 예측 방법을 제공합니다:
방법 1:
- 1. SMA 길이를 3으로 설정하고 1 막대만큼 과거로 이동시킵니다. 이렇게 설정하면 이동된 SMA는 마지막 막대(Bar = 0)에서만 존재하지 않으며, 다음 미래 가격 Close[-1]의 값이 필요합니다.
- 2. SMA 필터의 채널 폭을 계산합니다. 호드릭-프레스콧 필터와 동일하게 설정합니다. lambda를 찾습니다.
- 3. 마지막 막대에서 호드릭-프레스콧 필터 값 HP[0]를 계산하고, 동일한 값이 SMA[0]에서 주어지는 것으로 가정합니다.
- 4. Close[-1] = 3*HP[0] - Close[0] - Close[1]을 찾습니다.
- 5. SMA 길이를 5로 늘리고 모든 계산을 반복하여 Close[-2] = 5*HP[0] - Close[-1] - Close[0] - Close[1] - Close[2]를 찾습니다. 이 과정을 지정된 미래 FutBars 가격 수만큼 반복합니다.
방법 2:
- 1. SMA 길이를 2*FutBars+1로 설정하고 SMA를 FutBars만큼 과거로 이동시킵니다.
- 2. SMA 필터의 채널 폭을 계산합니다. 호드릭-프레스콧 필터와 동일하게 설정합니다. lambda를 찾습니다.
- 3. 마지막 FutBars에서 호드릭-프레스콧 필터 값을 계산하고, 새로운 가격이 나타날 때 SMA가 유사하게 동작한다고 가정합니다.
- 4. Close[-1] = (2*FutBars+1)*HP[FutBars-1] - Sum(Close[i],i=0..2*FutBars-1), Close[-2] = (2*FutBars+1)*HP[FutBars-2] - Sum(Close[i],i=-1..2*FutBars-2) 등을 찾습니다.
이 지표는 다음과 같은 입력값을 특징으로 합니다:
- Method - 예측 방법
- LastBar - 현재 가격을 바탕으로 예측을 확인할 마지막 막대 수 (LastBar >= 0)
- PastBars - 호드릭-프레스콧 필터가 계산되는 이전 막대 수 (많을수록 좋습니다, 또는 최소한 PastBars > 2*FutBars)
- FutBars - 예측된 미래 값의 수
이 지표는 예측된 값을 빨간색으로 강조합니다. 아래 예시는 방법 1을 사용했습니다:
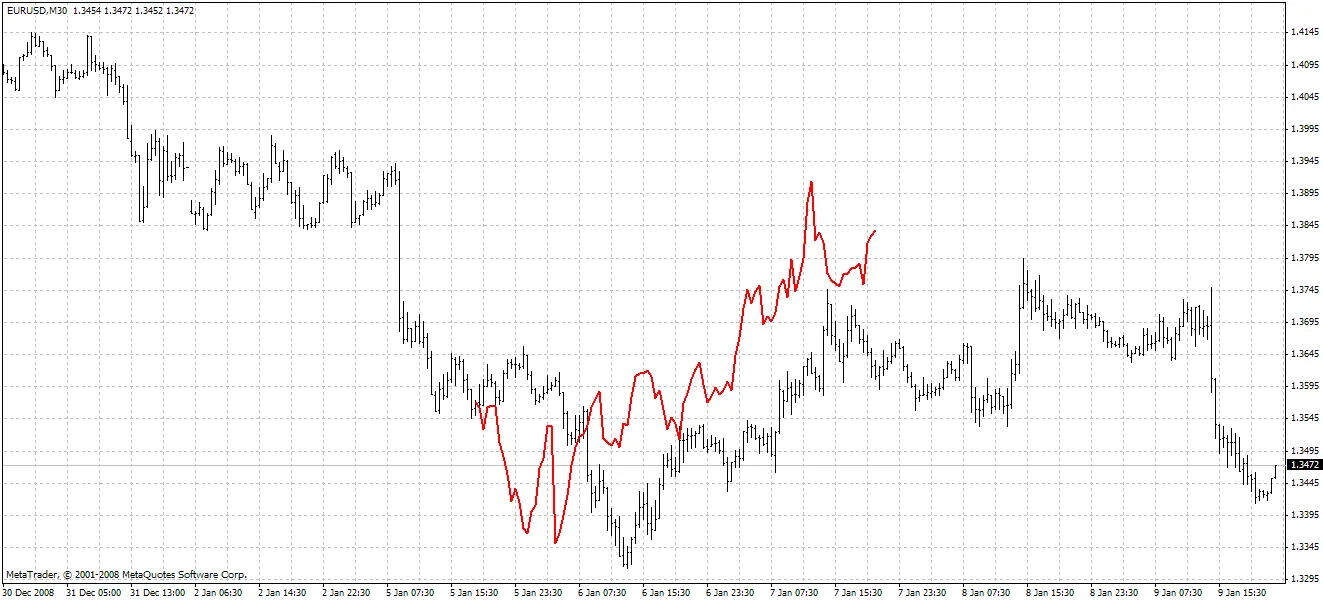
방법 2:
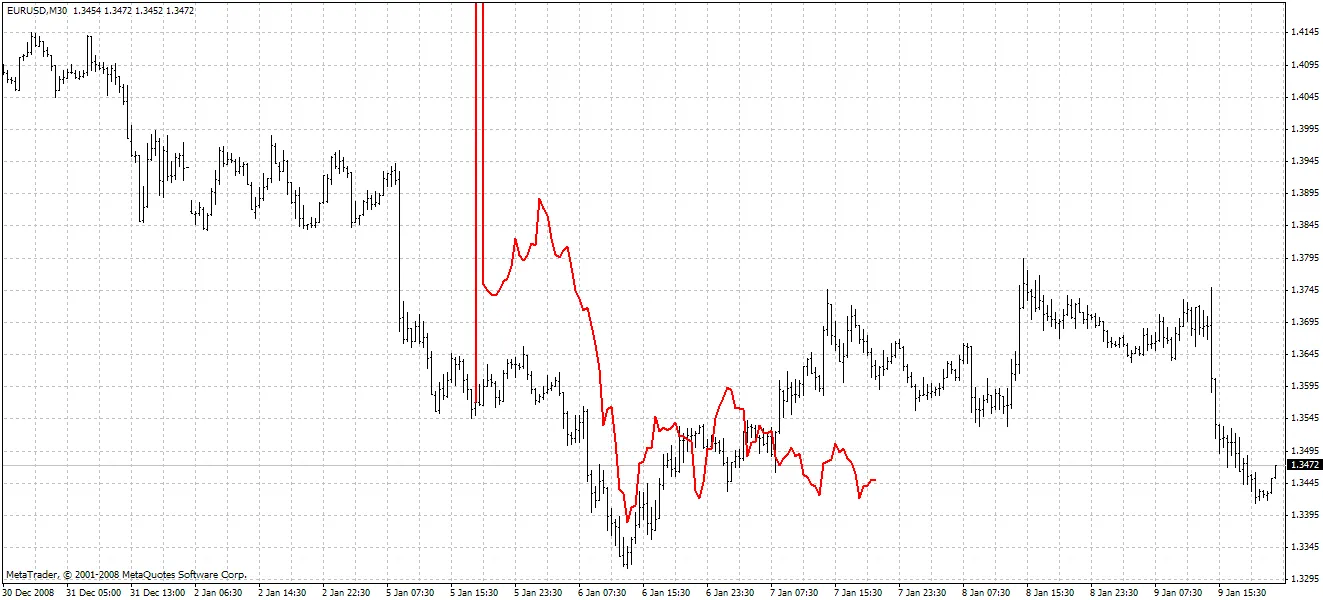
두 번째 방법은 더 정확하지만, 종종 첫 번째 예측 가격에서 큰 스파이크가 발생합니다. 설명된 예측 방법은 호드릭-프레스콧 필터에 더 가까운 주파수 매개변수를 가진 FIR 필터를 탐색하여 개선할 수 있습니다. 예를 들어, SMA 대신 Hanning, Blackman, Kaiser와 같은 상수 지연을 가진 필터를 시도할 수 있습니다.
저자는 아래 포럼 섹션에 게시된 원래 호드릭-프레스콧 필터 지표에 대해 사용자 Korey에게 감사드립니다:

댓글 0