作者:gpwr
版本历史:
2009年6月26日 - 添加了新的指标 BPNN Predictor with Smoothing.mq4,使用EMA平滑价格后进行预测。
2009年8月20日 - 修正了计算神经元激活函数的代码,防止算术异常;更新了 BPNN.cpp 和 BPNN.dll。
2009年8月21日 - 在DLL执行结束时添加了内存清理;更新了 BPNN.cpp 和 BPNN.dll。
神经网络简要理论:
神经网络是一个可调节的输出模型,作为输入的函数。它由多个层组成:
- 输入层,包含输入数据
- 隐含层,由称为神经元的处理节点组成
- 输出层,由一个或多个神经元组成,其输出即为网络输出。
相邻层的所有节点都是互相连接的。这些连接称为突触。每个突触都有一个指定的缩放系数,通过这个系数,数据在突触中传播时会被放大。这个缩放系数被称为权重 (w[i][j][k])。在前馈神经网络(FFNN)中,数据从输入传播到输出。下面是一个包含一个输入层、一个输出层和两个隐含层的FFNN示例:
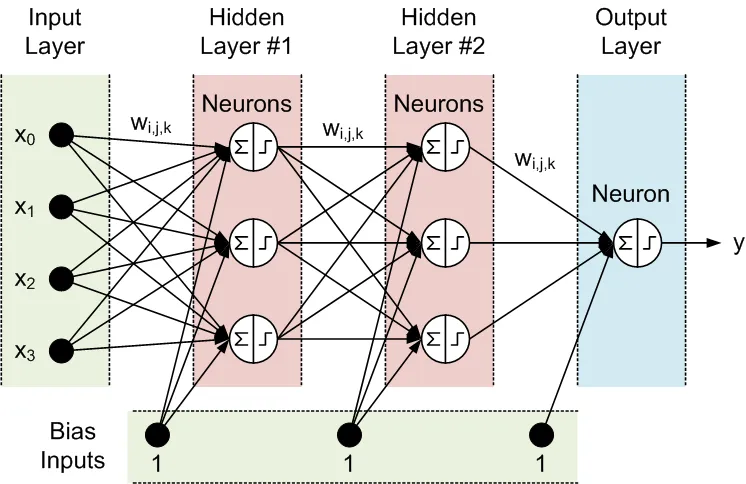
FFNN的拓扑结构通常缩写为:<输入数量>-<第一个隐含层的神经元数量>-<第二个隐含层的神经元数量>-...-<输出数量>。上述网络可称为4-3-3-1网络。
数据由神经元通过两个步骤处理,分别在圆圈内通过求和符号和阶梯符号表示:
- 所有输入乘以相关的权重并求和
- 结果和通过神经元的激活函数处理,输出为神经元的输出。
正是神经元的激活函数赋予了神经网络模型非线性。没有它,隐含层就没有意义,神经网络将变成线性自回归(AR)模型。
附带的库文件为NN功能提供了三种激活函数供选择:
- sigmoid sigm(x)=1/(1+exp(-x)) (#0)
- 双曲正切 tanh(x)=(1-exp(-2x))/(1+exp(-2x)) (#1)
- 有理函数 x/(1+|x|) (#2)
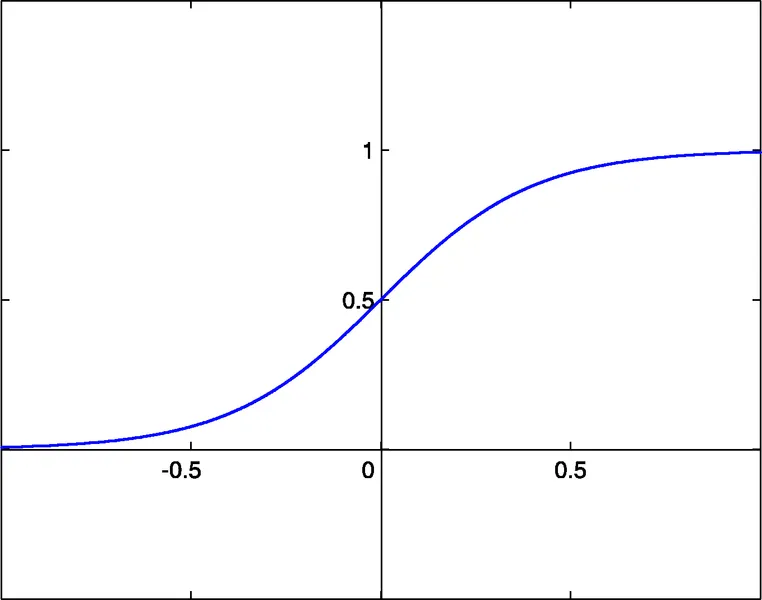
这些函数的激活阈值为 x=0。通过每个神经元的额外输入,称为偏置输入,这个阈值可以沿x轴移动,这个偏置输入同样有一个权重分配给它。
输入、输出、隐含层的数量、层内的神经元数量,以及突触权重的值完全描述了一个FFNN,即它创建的非线性模型。为了找到权重,网络必须经过训练。在监督训练中,多个过去的输入集和相应的期望输出被输入到网络中。权重被优化以达到网络输出与期望输出之间的最小误差。权重优化的最简单方法是误差反向传播,这是一种梯度下降方法。附加的训练函数 Train() 使用了这种方法的变体,称为改进的弹性反向传播加(iRProp+)。这个方法的详细信息可以在这里找到:
http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.17.1332
梯度优化法的主要缺点是它们往往会找到局部最小值。对于像价格序列这样的混乱序列,训练误差表面具有非常复杂的形状,包含许多局部最小值。对于这种序列,遗传算法是一种更优的训练方法。
附带文件:
- BPNN.dll - 库文件
- BPNN.zip - 编译 BPNN.dll 所需的所有文件压缩包
- BPNN Predictor.mq4 - 预测未来开盘价格的指标
- BPNN Predictor with Smoothing.mq4 - 预测平滑开盘价格的指标
文件 BPNN.cpp 包含两个函数:Train() 和 Test()。Train() 用于根据提供的过去输入和期望输出值训练网络。Test() 用于使用优化后的权重计算网络输出。
以下是 Train() 的输入(绿色)和输出(蓝色)参数列表:
double inpTrain[] - 输入训练数据(1D数组,包含2D数据,旧数据在前)
double outTarget[] - 用于训练的输出目标数据(2D数据,作为1D数组,旧数据在前)
double outTrain[] - 输出1D数组,用于存放训练中的网络输出
int ntr - 训练集数量
int UEW - 是否使用外部权重初始化(1=使用 extInitWt,0=使用随机)
double extInitWt[] - 输入1D数组,用于存放外部初始权重的3D数组
double trainedWt[] - 输出1D数组,用于存放训练后的权重的3D数组
int numLayers - 包含输入、隐含和输出的层数
int lSz[] - 各层神经元数量。lSz[0]为网络输入数量
int AFT - 神经元激活函数类型(0:sigm,1:tanh,2:x/(1+x))
int OAF - 是否启用输出层的激活函数;1启用,0禁用
int nep - 最大训练轮数
double maxMSE - 最大均方误差;训练在达到 maxMSE 后停止
以下是 Test() 的输入(绿色)和输出(蓝色)参数列表:
double inpTest[] - 输入测试数据(2D数据,作为1D数组,旧数据在前)
double outTest[] - 输出1D数组,用于存放训练中的网络输出(旧数据在前)
int ntt - 测试集数量
double extInitWt[] - 输入1D数组,用于存放外部初始权重的3D数组
int numLayers - 包含输入、隐含和输出的层数
int lSz[] - 各层神经元数量。lSz[0]为网络输入数量
int AFT - 神经元激活函数类型(0:sigm,1:tanh,2:x/(1+x))
int OAF - 是否启用输出层的激活函数;1启用,0禁用
是否在输出层使用激活函数(OAF参数值)取决于输出的性质。如果输出是二进制的,这在分类问题中很常见,那么在输出层应该使用激活函数(OAF=1)。请注意,激活函数#0(sigmoid)有0和1的饱和水平,而激活函数#1和#2则有-1和1的水平。如果网络输出是价格预测,那么在输出层不需要激活函数(OAF=0)。
使用NN库的示例:
BPNN Predictor.mq4 - 预测未来开盘价格。网络的输入是相对价格变化:
x[i]=Open[test_bar]/Open[test_bar+delay[i]]-1.0
其中 delay[i] 计算为斐波那契数(1,2,3,5,8,13,21..)。网络的输出是下一个价格的预测相对变化。输出层关闭了激活函数(OAF=0)。
指标输入:
extern int lastBar - 过去数据中的最后一根柱子
extern int futBars - 未来要预测的柱子数量
extern int numLayers - 包含输入、隐含和输出的层数(2..6)
extern int numInputs - 输入数量
extern int numNeurons1 - 第一隐含层或输出层的神经元数量
extern int numNeurons2 - 第二隐含层或输出层的神经元数量
extern int numNeurons3 - 第三隐含层或输出层的神经元数量
extern int numNeurons4 - 第四隐含层或输出层的神经元数量
extern int numNeurons5 - 第五隐含层或输出层的神经元数量
extern int ntr - 训练集数量
extern int nep - 最大轮数
extern int maxMSEpwr - 设置最大MSE=10^maxMSEpwr;训练在
指标在图表上绘制三条曲线:
- 红色 - 未来价格的预测
- 黑色 - 过去训练的开盘价格,作为网络的期望输出
- 蓝色 - 训练输入的网络输出
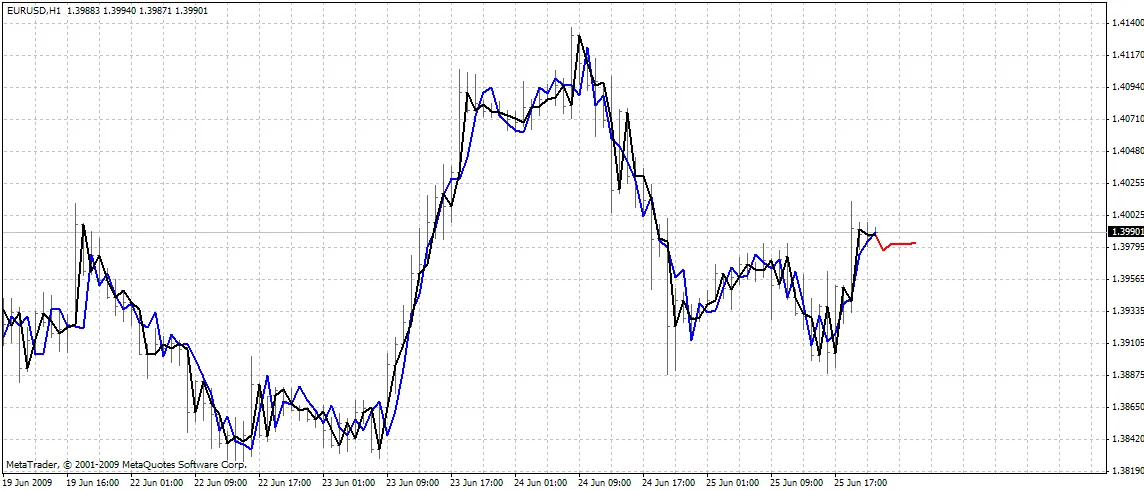
BPNN Predictor.mq4 - 预测未来平滑的开盘价格。它使用 EMA 平滑,周期为 smoothPer。
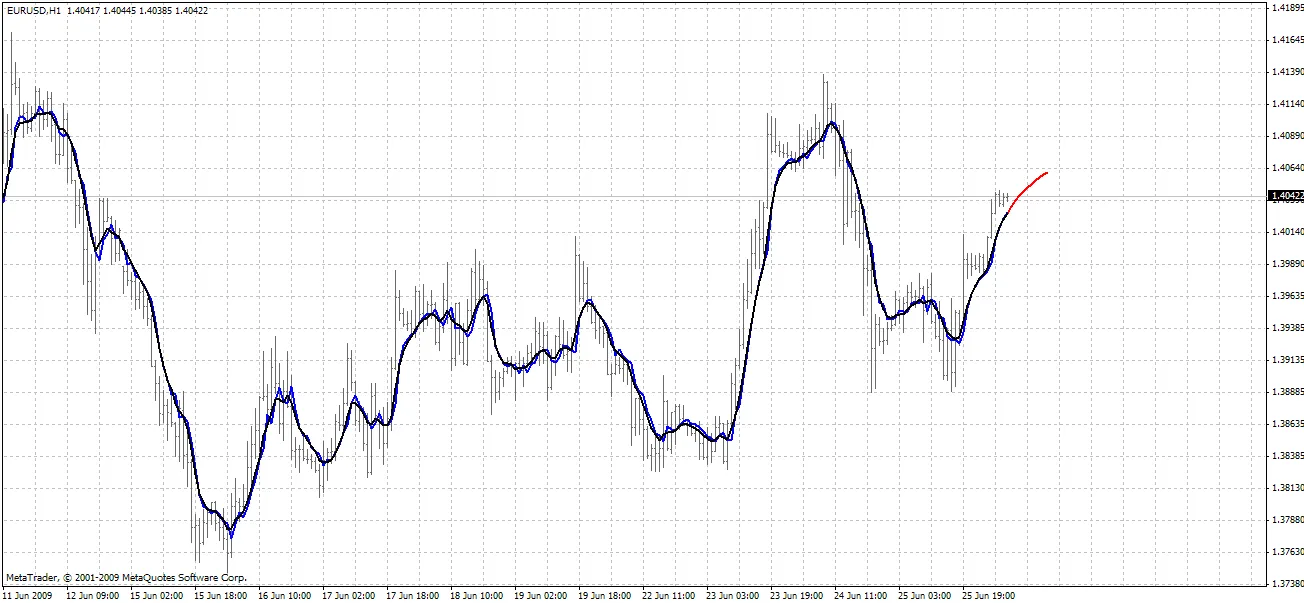
设置步骤:
- 将附带的 BPNN.DLL 复制到 C:\Program Files\MetaTrader 4\experts\libraries
- 在MetaTrader中:工具 - 选项 - 交易顾问 - 允许DLL导入
您也可以使用 BPNN.zip 中的源代码编译自己的 DLL 文件。
建议:
- 一个有三层的网络(numLayers=3:一个输入层、一个隐含层和一个输出层)对于绝大多数情况已经足够。根据 Cybenko 定理(1989),一个具有一个隐含层的网络能够以任何期望的精度逼近任何连续的多变量函数;而一个具有两个隐含层的网络能够逼近任何不连续的多变量函数:
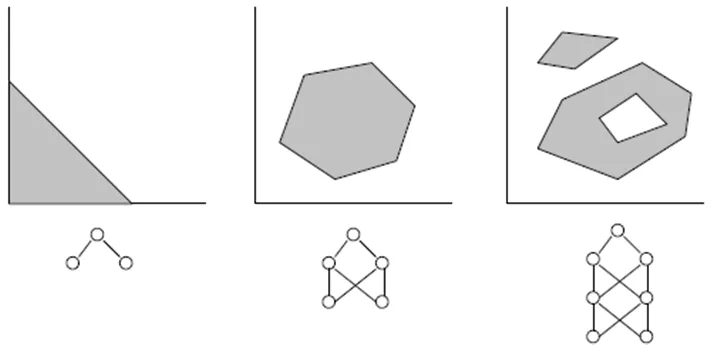
- 隐含层中神经元的最佳数量可以通过试验得出。文献中可以找到以下“经验法则”:隐含神经元数量 = (输入数量 + 输出数量)/2,或者 SQRT(输入数量 * 输出数量)。请注意训练误差,由指标在MetaTrader的专家窗口报告。
- 为了实现泛化,训练集数量(ntr)应该选择为网络中权重总数的2-5倍。例如,默认情况下,BPNN Predictor.mq4 使用的是一个12-5-1的网络。权重总数为(12+1)*5+6=71。因此,训练集数量(ntr)至少应为142。泛化和记忆(过拟合)的概念在下面的图中进行了说明。
- 网络的输入数据应转换为平稳的。外汇价格并不是平稳的。同时建议将输入归一化到-1..+1的范围内。
下图显示了一个线性函数y=b*x(x-输入,y-输出),其输出受到噪声的干扰。这种添加的噪声导致函数测量输出(黑点)偏离直线。函数y=f(x)可以通过前馈神经网络建模。具有大量权重的网络可以完美拟合测量数据,误差为零。其行为呈现为通过所有黑点的红色曲线。然而,这条红色曲线与原始线性函数y=b*x(绿色)没有任何关系。当这个过拟合的网络用于预测函数y(x)的未来值时,由于随机噪声,将会产生巨大的误差。
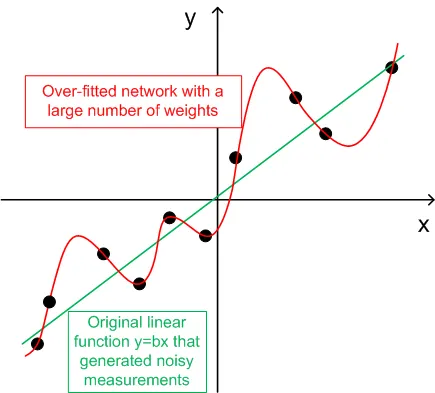
为了分享这些代码,作者有个小小的请求。如果您能基于这些代码创建出盈利的交易系统,请通过电子邮件直接与我分享您的想法,邮箱:vlad1004@yahoo.com。
祝您好运!

评论 0